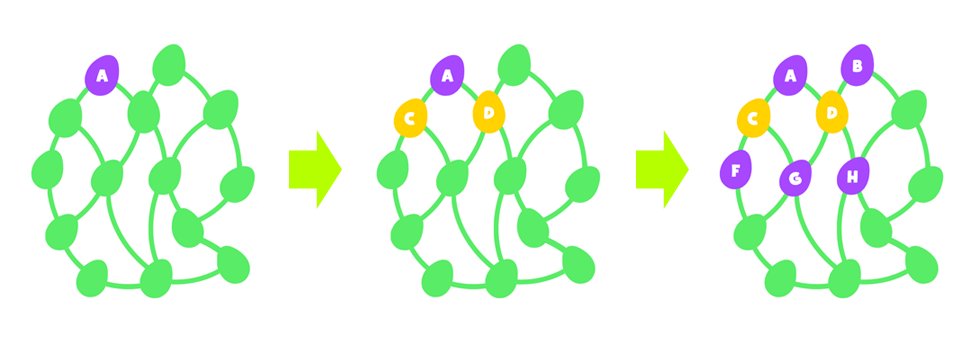
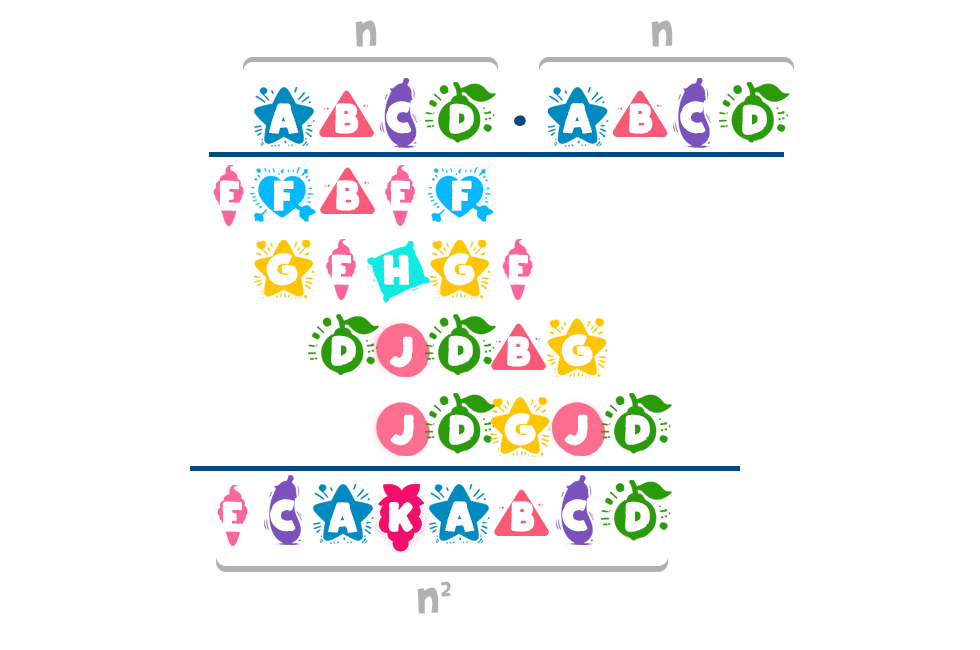
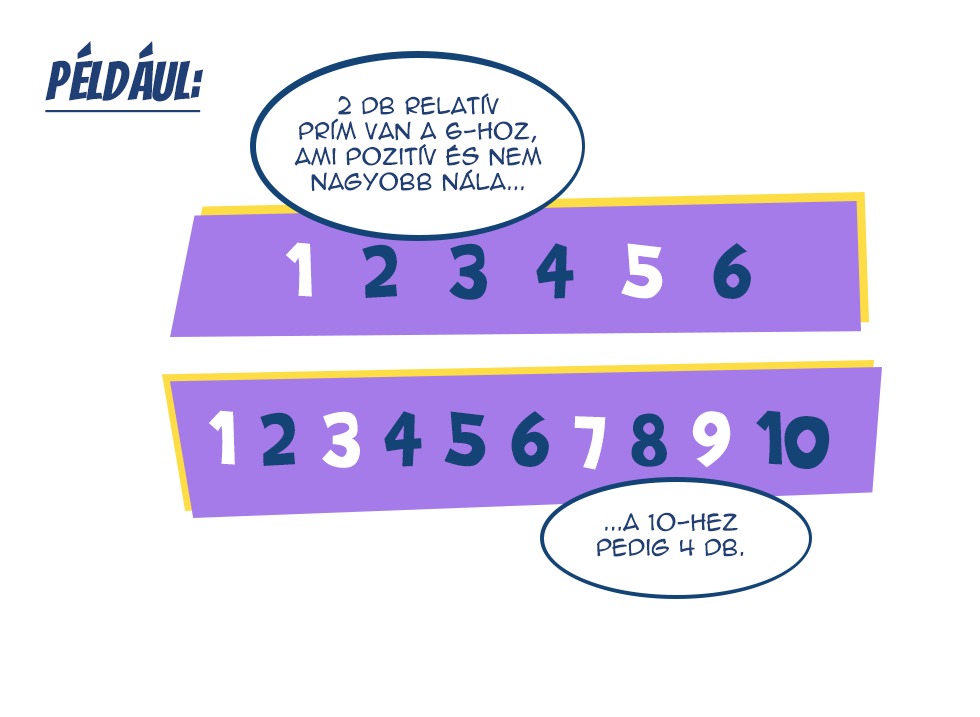
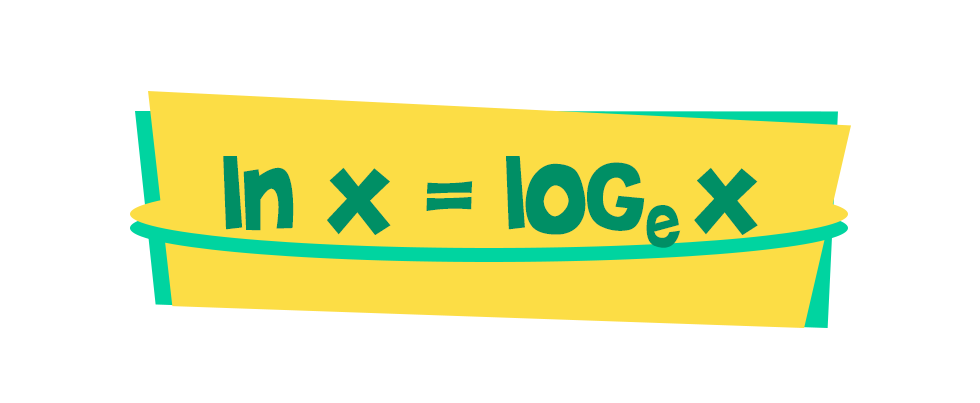Kalózok és holdacska
Kalózok és holdacska
A matematika egyik legendás és egyben elátkozott problémája a kör négyszögesítése, azaz egy olyan négyzet megszerkesztése, ami egy adott kör területével megegyező területű. A remény a feladvány megoldására legkésőbb 1882-ig, a p transzcendens voltának bizonyításáig (ami Ferdinand von Lindemann nevéhez köthető) élhetett, ami azonban véget vetett az álmoknak.
A probléma felvetődése időben jóval korábbra tehető, m ár az ókori ...