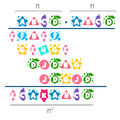
Következzen a "Díszítsd fel a fát!" feladat egy megoldása.

Az alapötlet, hogy megvizsgáljuk a háromszög oldalaira írandó számokat néhány egyszerű oszthatósági szempont alapján.

3-mal való oszthatóság

Először is, észrevehetjük, hogy az elhelyezendő számok összege 285. Másrészt, a háromszög csúcsaiba kerülő számok két-két oldal összegéhez is hozzájárulnak, azaz, ha vesszük a három oldalösszeg (x) összegét, abba ezek duplán számítanak bele.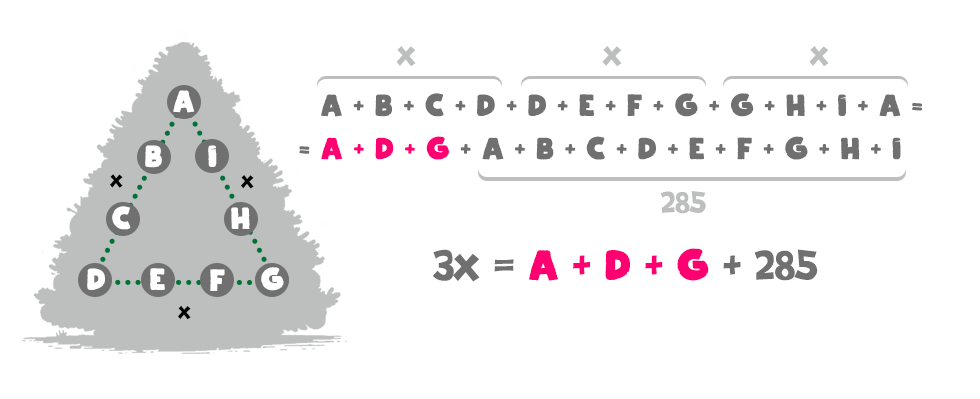Mivel a 285 és a 3x is osztható 3-mal, ennek a csúcsokba kerülő számok összegére is teljesülnie kell, azaz a 3 osztója az A+D+G összegnek.

A számaink a 3-mal való oszthatóság tekintetében két csoportba oszthatók, a 9, 36, 81 osztható 3-mal, az 1, 4, 16, 25, 49, 64 pedig 3-mal osztva 1 maradékot ad. A számok közül tehát csak úgy választhatunk három olyat, melyek összege 3-mal osztható, ha vagy eleve mindhárom kiválasztott szám osztható 3-mal, vagy 3-mal osztva mindhárom 1 maradékot ad (hisz ekkor a három 1-es maradék épp kiad egy 3-ast.)

Ha mindhárom szám 3-mal osztható (nevezzük ezeket egyszerűen 3k alakú számoknak valamilyen egész k-ra), akkor az azt jelentené, hogy a három csúcs a 9, 36, 81. Ekkor 3x = 9+36+81 + 285, amiből az egy oldalon lévő számok összegére x=137-et kapunk. Ez a forgatókönyv viszont nem lehetséges, mert a 9 és 81 közé ez esetben két olyan szám kellene a megmaradók (azaz az 1, 4, 16, 25, 49, 64) közül, melyek összege 47, ami sehogy sem jön ki.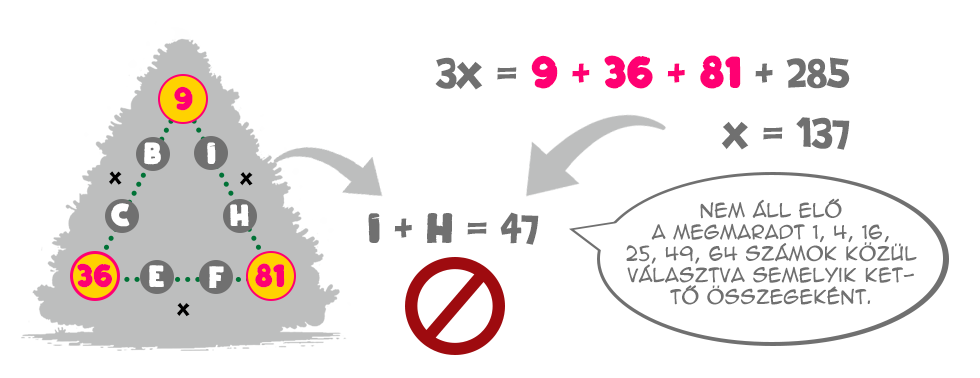Következésképpen a három csúcsba 3-mal osztva 1 maradékot adó (3k+1 alakú) szám, vagyis az 1, 4, 16, 25, 49, 64 közül valamelyik három kerül, a 9, 36, 81 pedig valamelyik oldal(ak) belsejébe.

4-gyel való oszthatóság

Hasonlóan vizsgálhatjuk a 4-gyel való oszthatóságot. A számaink közül a 4, 16, 36, 64 oszthatók 4-gyel (4k alakúak), az 1, 9, 25, 49, 81 pedig egyaránt 1-1 maradékot adnak 4-gyel osztva (4k+1 alakúak).

Ha minden csúcsba 4-gyel osztható szám kerülne, akkor a 2-2-2 belső helyre egy 4k és öt 4k+1 alakú szám maradna, amit viszont nem tudnánk egyenlően szétosztani. (4-gyel osztva eltérő maradékok keletkeznének legalább két oldalon, így az összeg is eltérne.)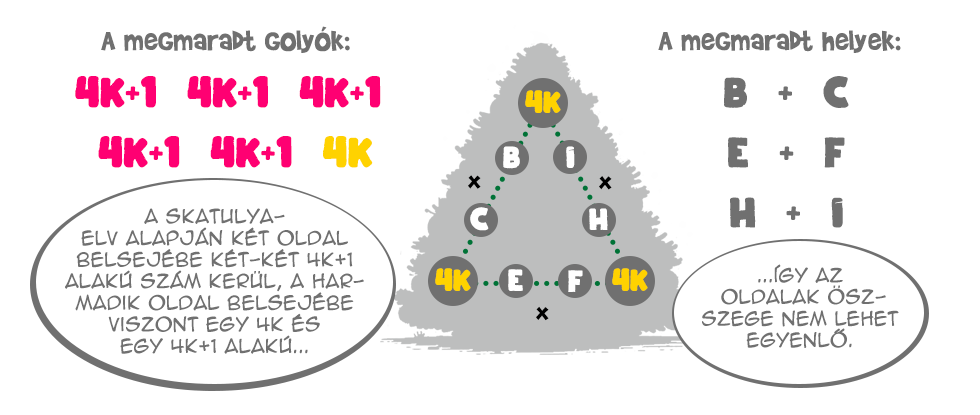

Hasonlóan ellentmondásba futunk, ha legalább két csúcs 4k+1 alakú. Az eredeti számok 4-gyel vett osztási maradékainak összege 5. A csúcsokban lévők – mint korábban láttuk – duplán számítanak, így ha mindhárom csúcs 4k+1 alakú, akkor ez az összeg 8-ra, ha két csúcs 4k+1 alakú, akkor pedig 7-re módosul. Bármelyik eset is áll fenn, a maradékokat is három egyenlő részre kellene osztanunk, de sem a 8, sem a 7 nem oszthatók 3-mal.

Ha két 4k alakú csúcsunk van, akkor viszont van egy lehetséges forgatókönyv:Összegezve az eddigieket, a 4k alakú számok közül – a 3-mal való oszthatóságnál látottak miatt – a 36 nem szerepelhet csúcsban, tehát a többi, azaz a 4, 16, 64 közül valamely kettőnek muszáj. A 4k+1 alakúakból pedig szintén a korábbiak alapján a 9 és a 81 nem kerülhet csúcsba, azaz az 1, 25, 49 közül az egyiknek kell.

5-tel való oszthatóság

A számaink 5-tel osztva három csoportba sorolhatók: 5-tel osztható (azaz 5k alakú) a 25, 5k+1 alakú az 1, 16, 36, 81, 5k-1 alakú pedig a 4, 9, 49, 64. A maradékok összege így épp 0 (hisz a 285 osztható 5-tel.)

Ha a 25 nem csúcs, akkor a háromszög őt tartalmazó oldalán a maradékok összege 0+1+1+1, 0+1+1+(-1), 0+1+(-1)+(-1) vagy 0+(-1)+(-1)+(-1), azaz 3, 1, -1 vagy -3. A másik két oldalon lehetséges maradékösszegek viszont hasonló módon megkapva a -4, -2, 0, 2, 4, vagyis biztosan eltérnek az 5-höz tartozó oldal összegétől. Következésképpen a 25 valamelyik csúcsba kell, hogy kerüljön, ráadásul a 4-gyel való oszthatóságnál látottak alapján ez lesz a 4k+1-es csúcs. Ezek alapján pedig a két 4k alakú csúcs a 4, 16, a 4, 64 vagy a 16, 64 pár lesz.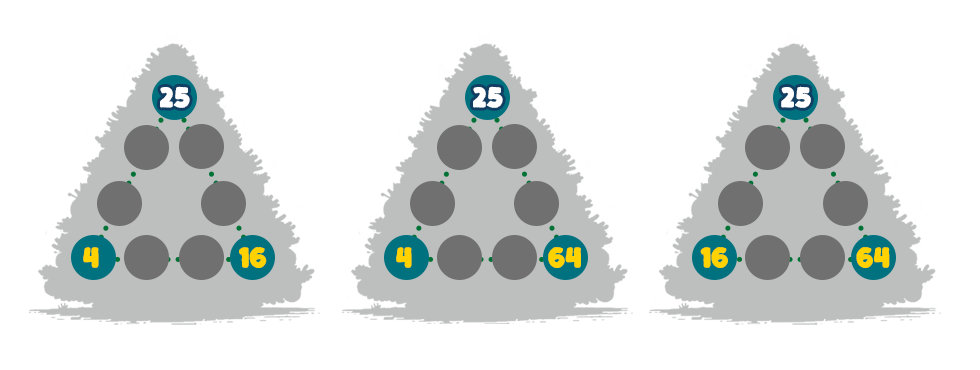Ha a három csúcs a 25, 4, 16, akkor 3x = 25+4+16 + 285 = 330, amiből az egy oldalon lévő számok összege 110 kell, legyen. A 25 és 16 közti oldalon tehát még 69-et kell kirakni az 1 9, 36, 49, 64, 81 számokból kettő összegeként, de ez lehetetlen.

Ha a csúcsok a 25, 16, 64, akkor 3x = 25+16+64 +285 = 390, azaz az oldalakon lévő összeg 130. A 25 és 64 közti oldalon ez még 41-et jelentene az 1, 4, 9, 36, 49, 81 számokból szintén kettővel, de ez sem lehetséges.

Marad tehát egyetlen lehetőségként, hogy a csúcsokban a 25, 4 és a 64 szerepel. Ekkor 3x = 25+4+64 + 285 = 378, amiből x=126.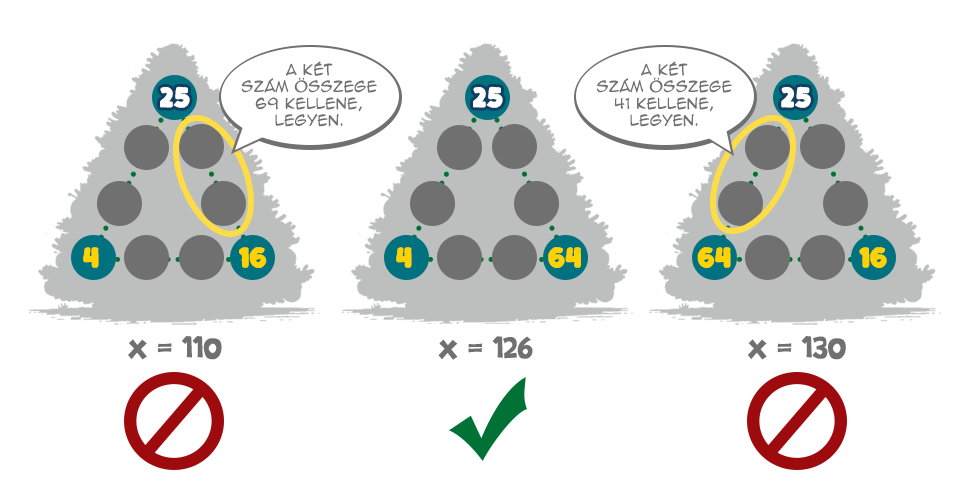Így a 25 és 64 közé 37-es összegnek kell kerülnie, ami csak 1+36-ként lehetséges. A 25 és 4 közé 97-nek, ami 16+81. Míg végül a 4 és 64 közé 58-as összegnek, ami a 9+49-ként lehet.