Egy visszahúzódó fiatal lány, egy véres forradalom, egy gazdag könyvtár és egy ókori történet. Többek közt ezek az összetevők kellettek ahhoz, hogy felgyulladjon a megszállottság a romantika korának egyik legérdekesebb matematikusának szívében és fejében. Ő volt Marie-Sophie Germain, alias Monsieur Le Blanc, a számelmélet felemelkedését is elhozó időszak egyik elfeledett alakja, aki életének minden nehézsége ellenére komoly érdemeket tudhat magáénak a matematika e területén.

Forradalom és Arkhimédész

A kis Sophie 1776-ban született egy jómódú kereskedőcsalád második gyermekeként. Apja aranyműves, ékszerész és selyemkereskedő, anyja pedig egy aranyműves leánya volt. E kettő elég okot szolgáltatott arra, hogy a család minden tagjának bizonyos fokig el kelljen sajátítania a számtant, hogy szükség esetén közreműködhessenek a számlák, nyilvántartások kezelésében. Sophie érdeklődését azonban az üzleti világ helyett sokkal inkább a természettudományok, azok közül is főként a matematika és a fizika ragadta meg.

A nagy francia forradalom idején, míg édesapja aktív részese volt a politikai eseményeknek, az ifjú Sophie az apa könyvtárában lelt menedéket. Itt bukkant rá Jean-Étienne Montucla A matematika története című könyvére is, melyben többek között Arkhimédészről is olvashatott. A lány csodálattal állt az ókori tudós matematika iránti szenvedélyének mértéke előtt. A fennmaradt források szerint Arkhimédész időnként annyira belefeledkezett a matematikába, hogy még enni és inni is elfelejtett, szolgáinak kellett emlékeztetniük ezen alapvető szükségleteinek kielégítésére. Sőt, még halálakor sem volt hajlandó felhagyni matematikai tevékenységével, ami a legenda szerint az életébe került (lásd „Ne zavard a köreimet!”). Arkhimédész példája Sophie-nak is utat mutatott. Talált végre valamit, amiben igazán el tudott mélyülni, amibe el tudott menekülni a forradalom szörnyűségei elől.Később más, szintén matematikával foglalkozó könyvek is a kezébe akadtak, ekkortájt ismerkedett meg például az analízissel, valamint Newton és Euler korábbi munkáival is. Szülei kezdetben nem igazán nézték jó szemmel a matematika iránti szerelmét. Apja és anyja sokszor fosztották meg esténként a tűztől és a gyertyafénytől, így nehezítve lányuk dolgát, aki azonban nem adta fel egykönnyen, gyertyákat csempészett a szobájába, hogy titokban tovább olvashasson. A fáma szerint, egy reggelen a könyvtárban találtak rá, az egyik könyvébe borulva aludt. A helyiségben olyan hideg volt, hogy a tinta belefagyott a tartójába. Ez az esemény azonban végre megenyhítette szülei szívét, sőt, apja később egész életében támogatta lányát, hogy az minden idejét és energiáját a matematikának szentelhesse.

Monsieur Le Blanc

Hiába az érdeklődés és a tehetség, nőként, illetve ugyan jómódú, de nem nemesi származása miatt Sophie messze nem kaphatott olyan képzést, amilyet szeretett volna. Épp 18 éves volt a párizsi műszaki egyetem, az École Polytechnique alapításakor, mégsem volt esélye bekerülni a neves intézménybe. Persze ezúttal sem adta fel.

Az egyetem lehetővé tette a kurzusokon való részvételt levelező hallgatóként is. Az ifjú hölgynek némi trükkel élve, Monsieur Le Blanc álnéven sikerült hozzáférnie az előadások jegyzeteihez, köztük Joseph Louis Lagrange, a számelmélet egyik óriásának analízis kurzusáéhoz is. A férfinak némileg gyanús volt a dolog, ugyanis az álnév egy létező hallgatójának neve volt, aki viszont, finoman szólva, nem volt túl erős matematikából. Amikor Sophie megírta az előadásokkal kapcsolatos észrevételeit, azok minősége nem igazán illet Lagrange, az igazi Antoine-August LeBlanc-ról kialakított képébe. A tanár nem nyugodott bele, személyesen is találkozni kívánt Monsieur Le Blanc-nal, így végül fény derült a titokra. Lagrange pozitívan fogadta az igazságot, és szárnyai alá vette a lányt, sajnos azonban minden igyekezete ellenére rendszerszerű oktatást ő sem biztosíthatott neki.

Sajátos és esetleges tanulmányai folytatásaként Sophie mélyebben elmerült a másik neves számelmélész, Adrien-Marie Legendre és a nagy Carl Friedrich Gauss számelméleti munkáiban is. Legendre és közte később rendszeres levelezés is kialakult, ami aztán komoly együttműködéssé fejlődött, melyet leginkább a Fermat-sejtéssel kapcsolatos munkáik tanúsítanak.

Gaussnak szintén a Le Blanc álnevet használva írt leveleket. Kezdetben ezek tárgya a német zseni méltatása volt, később azonban Sophie a számelméleti eredményeivel elnyerte a géniusz elismerését. E tisztelet azután sem változott meg, hogy Gauss tudomást szerzett Monsieur Le Blanc valódi kilétéről. Erre akkor került sor, amikor a napóleoni háborúk időszakában Gauss szülővárosa francia megszállás alá került, és Sophie emlékezve Arkhimédész sorsára, egy francia tábornok ismerősén, Joseph-Marie de Pernety-n keresztül próbált Gauss biztonságáról gondoskodni. A lány a félreértések elkerülése végett kénytelen volt levélben színt vallani Gaussnak, ezzel azonban még inkább elnyerte a férfi tiszteletét. Részlet Gauss leveléből:

"De hogyan is írhatnám le Önnek csodálatomat és megdöbbenésemet, amikor látom, hogy nagyra becsült levelezőtársam, M. LeBlanc átalakul e jeles személyiséggé, aki ily ragyogó példát mutat arra, amit én csak oly nehezen tudnék elhinni...

...e fenséges tudomány varázslatos varázsa csak azok előtt tárul fel, akiknek van bátorságuk mélyen belemerülni..."

Chladni ábrái

Az 1808-as év újabb mérföldkövet jelentett Sophie számára. Ebben az évben a porosz fizikus zenész és hangszerkészítő, Ernst Chladni Párizsban járt, és bemutatott néhány, a rezgő lemezekkel kapcsolatos kísérletet. Sophie itt találkozhatott először a Chladni nevét viselő porábrákkal. Az előadás témája kapcsán az Institut de France ki is írt egy pályázatot a rugalmas felületek rezgéseinek matematikai megalapozására, ami Sophie érdeklődését is felkeltette.

A verseny megkezdődött, de sokan már az elején feladták, mondván, a matematika akkori eszköztára nem elégséges a probléma megoldásához. Sophie azonban nem törődött bele ilyen könnyen. 1811-ben az övé volt az egyetlen érdemi pályázat, de nőként mégsem kaphatta meg a győztesnek járó díjat. Pályázatát nagyrészt amiatt támadták, hogy nem a fizika ismert alapelvein alapult, munkája mégis erős kiindulópontot jelentett a későbbi modellekhez. Olyannyira, hogy a verseny egyik bírája, Lagrange, kijavítva Sophie hibáit levezetett egy egyenletet, ami véleménye szerint jó eséllyel képes lehetett megadni Chladni mintázatait.

A határidőt meghosszabbították, de két év múlva ismét csak Sophie Germain volt az egyetlen érdemi pályázó. Igazolta, hogy Lagrange egyenlete több esetben valóban megadja a Chladni-ábrákat, de a lány hiányos oktatásának köszönhetően ezúttal sem tudta ezt kielégítően levezetni, ezért a munkájáért „csak” kitüntető díjat kapott.

Sophie ezúttal sem adta fel, újabb csiszolások után harmadszor is nekifutott. Ez a dolgozata, noha matematikailag némiképp még mindig hiányos volt, 1815-ben végül elnyerte a díjként kitűzött, 1 kg-os aranyérmet. A dolog pikantériája, hogy Sophie végül nem jelent meg a díj átadásán.

A versenyben fő riválisa Siméon Denis Poisson volt, aki képzettségének köszönhetően később Sophie munkájára támaszkodva részletesebben is kidolgozta az elméletet, mire azonban a rugalmasság témája bekerült a tudományos fősodorba, Sophie-t a közeg már kizárta magából. Tíz évvel később ugyan benyújtotta kiterjesztett kutatásait az Institut de France-nak, a bizottság – soraiban immár Poissonnal – nem vette figyelembe a dolgozatát. Az csak 1880-ban került kiadásra, amikor is Garpard de Prony, szintén egykori bizottsági tag, iratai között megtalálták.

A nagy terv

A rezgésekkel kapcsolatos munka mellett Sophie nem feledkezett meg a számelméletről sem. Ugyancsak ebben az időszakban szentelte idejének és energiáinak jelentős részét Pierre de Fermat már akkoriban is másfél évszázados sejtésének. Dióhéjban arról van szó, hogy az xⁿ+yⁿ=zⁿ egyenletnek – melynek n=2-re a pitagoraszi számhármasok mind eleget tesznek – nincs nemtriviális megoldása 2-nél nagyobb n-ek esetén az egész számok körében (triviálisan az x=y=z=0 mindig megoldás lesz). A sejtést ma már „nagy” Fermat-tétel (vagy Fermat utolsó tétele) néven emlegetjük, mivel 1995-ben Andrew Wiles publikálta több mint 100 oldalas bizonyítását. Noha Sophie csak részeredményekig jutott, egy bő évszázadig mégis az övé volt a legnagyobb elért eredmény a sejtés bizonyításában.

Sophie stratégiája alapvetően a következő volt. Először is azt akarta megmutatni, hogy minden páratlan p prímszám esetén végtelen sok olyan 2·N·p+1 alakú segédprím van (ahol N egy alkalmas egész szám), melyekkel elosztva az egész számok olyan hatványait, amiknek kitevője az eredetileg választott p, az osztások nullától különböző maradékai között nem lesznek egymást követő egész számok. Kicsit precízebben, ha x egy tetszőleges egész szám, akkor bármilyen páratlan p prímre az x^p mod (2Np+1) halmaz nem nulla elemei között nincsenek egymást követő egészek.

E furcsa tulajdonság következménye ugyanis, hogy ha lenne megoldása a Fermat-egyenletnek (x^p+y^p=z^p) a p páratlan prímkitevő esetén, akkor bármely fent említett segédprímnek osztania kellene az x, y, z valamelyikét.

A magyarázat a következő. Ha lenne olyan q segédprím, mely nem osztója x, y, z egyikének sem, akkor x, y, z mindegyikének lenne reciproka modulo q. Ez például az x esetén azt jelenti, hogy van olyan szám, amivel x-et megszorozva olyan számot kapunk, ami q-val osztva 1 maradékot ad. Például, ha q=7 lenne, akkor a 4 inverze a 2, mert 4·2=8 maradéka a 7-tel való osztás során 1. Jelöljük x reciprokát x^-1-nel. Ez biztosan nem a 0, szorozzuk meg hát a Fermat-egyenlet mindkét oldalát ennek p-edik hatványával. Így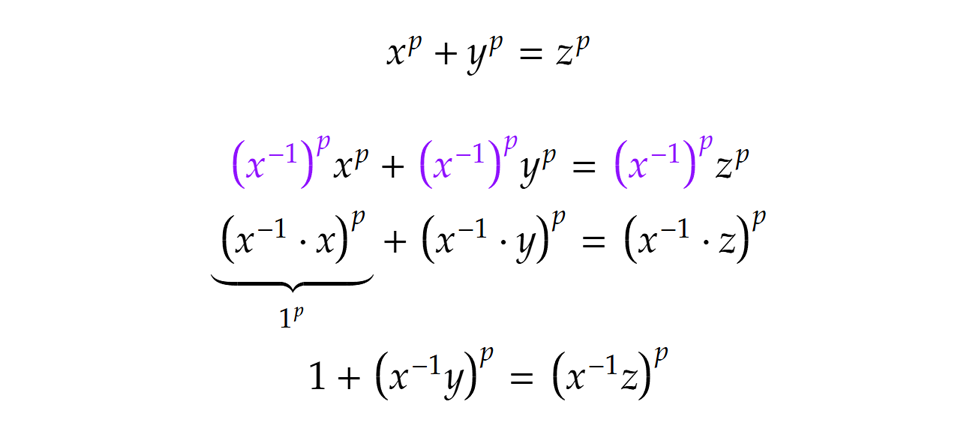ami épp azt jelenti, hogy x^-1y és x^-1z p-edik hatványainak maradékai a q-val való osztást követően egymás utáni számok, ami viszont ellentmond annak, hogy q egy alkalmas segédprím.

A kulcsgondolat most jön. Ha egy adott p esetén ez végtelen sok q segédprímre igaz lenne, akkor az x, y, z hármasból legalább az egyiknek végtelen sok prím osztója lenne a skatulya-elv alapján, így ez ellentmondana a számelmélet alaptételének, melynek egyik velejárója, hogy egy számot csak véges sok prím oszthat. A megkövetelt tulajdonság nem éppen nyilvánvaló, az ötlet mégis zseniális.

Példa

Válasszuk például a p=5-öt, és tekintsük az N=1 esetét. Ekkor 2Np+1=11, vagyis az egész számok ötödik hatványainak 11-gyel vett osztási maradékait kell vizsgálnunk. Valójában elég lesz az 1⁵, 2⁵, …, 10⁵-t megnéznünk, mert a 11-es hatványalaptól kezdve a maradékok már ismétlődnek. Kiszámolva ezeket egy mindössze kételemű halmazhoz jutunk, minden maradék 1 vagy 10. A lényeg viszont, hogy e halmaz nem tartalmaz egymást követő egészeket. Tehát p=5-re a 11 egy a fentiekben leírtaknak megfelelő segédprím.

Sajnos, ha N=2, akkor 2Np+1=21, ami nem prímszám (p továbbra is az 5), így ez az eset nem érdekes. Ha N=3, akkor 2Np+1=31, így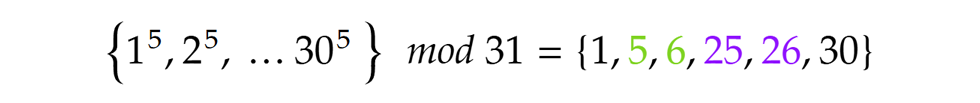Ez tartalmaz egymás utáni egészeket (ráadásul többet is), tehát a 31 nem megfelelő segédprím. Igazolható egyébként, hogy 3-mal osztható N választásakor ez mindig be fog következni, így az ilyen N-eket ettől kezdve nyugodtan át is ugorhatjuk.

Tovább folytatva a kísérletezést az N=4 esetben ismét találunk megfelelő segédprímet (ez a 41), de az 5, 6 esetén ismét csak nem. (Az N=5 esetén 2NP+1 nem prím, a 6 pedig ugye osztható 3-mal.) N=7-re a 71, aztán N=10-re a 101 ismét jók lesznek stb.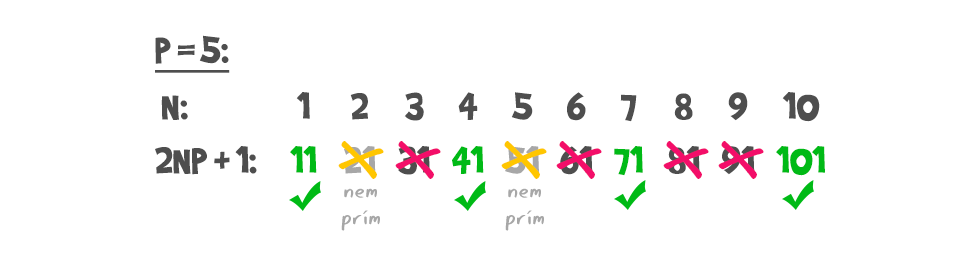Sophie következtetése szerint tehát, ha van megoldása a Fermat egyenletnek p=5-re, akkor x, y, z egyike a 11-nek, egyike a 41-nek, egyike a 71-nek, egyike a 101-nek (azaz a 2NP+1 modulusok) többszöröse, a skatulya-elv alapján pedig az ismeretlenek egyike legalább kettővel osztható az említett segédprímek közül.

A nagy kérdés, hogy minden páratlan prímre végtelen sok ilyen segédprím létezik-e. Ez esetben ugyanis, ha x, y, z a Fermat-egyenlet egy megoldása, akkor minden segédprím osztja x, y, z egyikét (ahogy a fenti példában), ez viszont azt jelentené, hogy legalább az egyiknek végtelen sok prím osztója van, ami ellentmondás, következésképpen kiinduló feltételezésünk, hogy az egyenletnek van megoldása, téves.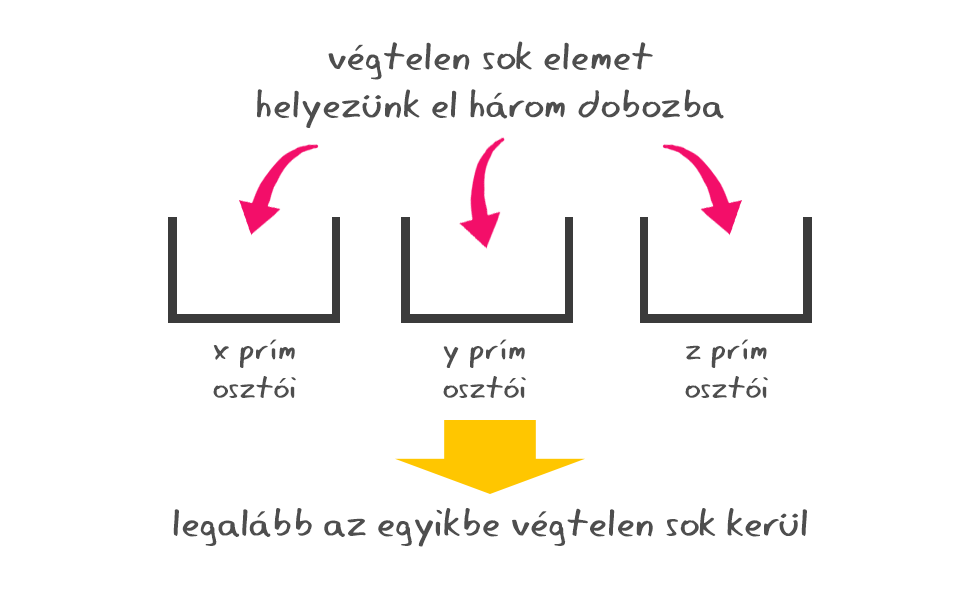Sajnos a nagy kérdésre a válasz a nem lett, minden esetben csak véges sok ilyen segédprím létezik. Maga Sophie vezette le, hogy például a p=3 esetén csak a 7 és a 13 felel meg a kritériumnak (bizonyítás itt).

Ijesztő számok

Sophie Germain ezúttal sem hagyta annyiban az ügyet. Egyik Gauss-nak írt leveléből tudjuk, hogy a későbbiekben eljutott addig a következtetésig, hogy páratlan prím kitevőjű esetben, ha van is megoldás, az viszonylag nagy szám kell, legyen. Precízebben, ha az x^p+y^p=z^p egyenletnek van egész megoldása, akkor az x+y, z-x, z-y egyike egyaránt osztható p^2p-1-nel és az összes olyan 2Np+1 alakú segédprím p-edik hatványával is, amire egyrészt teljesül a fent említett feltétel, másfelől p nem p-edik hatvány maradék modulo 2Np+1. Kissé komplikált, de nézzük ezt is konkrétabban.

A fenti példában p=5-re és N=1, 4, 7, 10-re láttuk, hogy az első feltétel teljesül, és mivel az 5 nem eleme a maradékok halmazának egyik esetben sem, így a második is. Sophie állítása alapján viszont akkor x+y, z-x, z-y egyike osztható lesz 5⁹-nel (5^2·5-1), illetve 11⁵-nel, 41⁵-nel, 71⁵-nel, 101⁵-nel, amiből következően ezek szorzatával is. Ebből adódóan viszont x, y, z egyike csak „ijesztően” nagy szám lehet.

Sajnos ez a tétele sem állta meg a helyét, minden próbálkozása ellenére sem sikerült kijavítania levezetésének hibáit, sőt, a fenti állítást azóta sem sikerült igazolnia senkinek. Annyit azért el lehet mondani, hogy ha valamilyen segédprímre teljesül a két feltétel, akkor x, y, z egyike osztható lesz p²-tel.

Még egy nekifutás

A sikertelen kísérletek ellenére (vagy éppen ezeknek is köszönhetően) végül Sophie-nak sikerült bebizonyítania a Fermat-sejtés állítását egy speciális esetre. E szerint olyan p páratlan prímekre, melyekre a 2p+1 is prím, az x^p+y^p=z^p egyenletnek nincs olyan megoldása, melyben az x, y, z egészek egyike sem osztható p-vel. Hosszú idő után ez volt az első jelentős lépés a sejtés bizonyításában. A tétel azóta Sophie Germain nevét viseli, illetve a fent említett tulajdonsággal bíró prímeket a szakirodalom Sophie Germain-prímeknek vagy egyszerűen csak Germain-prímeknek hívja.

Sophie eredményének köszönhetően a Fermat-sejtést két esetre osztották fel. Innentől kezdve azt az esetet, mely szerint az xⁿ+yⁿ=zⁿ egyenletnek nem lehet olyan egész megoldása, amire x, y, z egyike sem osztható n-nel, a Fermat-sejtés I. esetének nevezték. A II. eset szerint nem lehet olyan megoldás, ahol a három ismeretlen közül pontosan az egyik osztható n-nel. (A többi eset nem érdekes, mert ha mindhárom osztható lenne n-nel, akkor egyszerűsíthető úgy az egyenlet, hogy legalább az egyik biztosan ne legyen az; a háromból pontosan kettő pedig nem lehet osztható az alapvető oszthatósági szabályok miatt.)

Sophie Germain tétele

A tétel eredetileg így szólt. Legyen p egy páratlan prím, és q egy 2Np+1 alakú (segéd)prím, melyekre teljesül, hogy:

1. nincs két egymást követő szám az egész számok p-edik hatványainak q-val vett osztási maradékai között (Igazolható, hogy e feltétel ekvivalens azzal, hogy ha az x^p+y^p+z^p összeg osztható q-val, akkor x, y, z valamelyike is osztható vele, tehát x, y, z ismeretlenek q-val való oszthatósága szükséges feltétele x^p+y^p+z^p q-val való oszthatóságának. A bizonyítás lényegében a feljebb már részletezett, reciprokot használó levezetés.)

2. p maga nem maradék semmilyen p-edik hatvány q-val történő osztásakor (azaz q-val osztva p és x^p eltérő maradékot ad bármilyen x egész számra)

Az állítás, hogy ekkor a Fermat-tétel I. esete teljesül p-re. (Pontosabban, ha van megoldás, akkor p²-nek – és ezáltal p-nek is – osztania kell az x, y, z valamelyikét.)

A tétel egy átfogalmazott, ismertebb változata, hogy ha p egy páratlan Germain-prím, akkor p osztója a Fermat egyenletben szereplő x, y, z valamelyikének, vagyis a Fermat-tétel I. esete igaz p-re.

Az állítás alapja, hogy a két fenti feltétel speciálisan biztosan fennáll, ha q=2p+1 alakú prím, a következők miatt. Mivel q prím, a kis Fermat-tétel értelmében, illetve q-1=2p miatt, minden q-nál kisebb pozitív a egészre: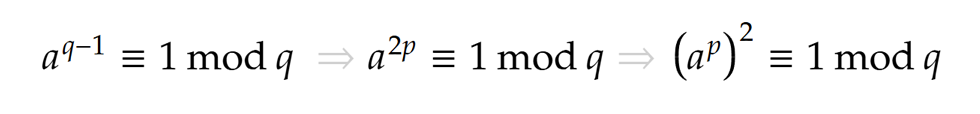így (a^p)²-1 = (a^p-1)·(a^p+1) osztható lesz q-val. Ez alapján viszont akkor a^p-1 vagy a^p+1 is osztható kell, legyen vele, hiszen q prím. Más szóval, a^p q-val osztva 1 vagy -1 maradékot ad.

Helyettesítsünk be „a” helyére x-et, y-t, z-t. Ha egyik sem osztható q-val, akkor az x^p+y^p+z^p összeg -3, -1, 1 vagy 3 maradékot ad a q-val való osztás során, mert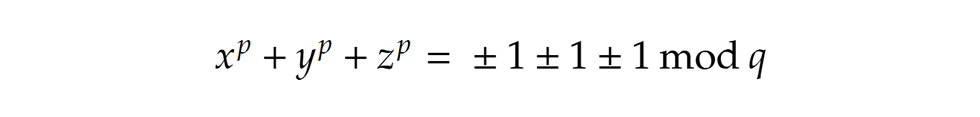Ez viszont azt jelenti, hogy a bal oldali összeg sem osztható q-val, így Sophie tételében teljesül az 1. feltétel.  Másfelől viszont a 2. feltétel is fennáll, hiszen x^p q-val osztva 1 vagy -1 maradékot ad, ami p-re nem teljesülhet, hisz p és q is páratlan prímek. A tétel állítása értelmében így ilyen p-re biztosan nincs olyan megoldása a Fermat-egyenletnek, melyben egyik ismeretlennek sem osztója p. A tétel részletes bizonyítása fellelhető itt, illetve itt is. 

Sophie egyébként ennél többet is megmutatott. Ha p és q olyan, hogy a 2 nem p-edik hatvány maradék modulo q, akkor teljesül az első feltétel, a segédprímek pedig 4p+1, 8p+1, 10p+1, 14p+1 vagy 16p+1 alakúak lesznek. Azokban az esetekben pedig, amikor a 2 egy p-edik hatvány maradék modulo q, sikerült megtalálnia az első feltételt kielégítő 2Np+1 alakú segédprímeket 1-től 10-ig terjedő N, és 100-nál kisebb páratlan prím p értékek esetén. Később azt is igazolta, hogy ezek mind kielégítik a 2. feltételt is.

A korszellem, illetve Sophie Germain képzettségének ebből fakadó hiányosságai miatt számos eredményét csak később ismerték el. Ezek közé tartozik az imént említett is, mely megtalálható Legendre 1823-as cikkében, de jó eséllyel Sophie tőle függetlenül vonta le következtetéseit, amit Legendre sosem tagadott. Mivel levelezésben álltak, minden bizonnyal megvitatták e kérdéseket, és ösztönzőleg hatottak egymásra, bizonyos értelemben tehát az érdemen is jogosan osztoznak. Mindenesetre kettejüknek együtt sikerült igazolniuk, hogy minden 197-nél kisebb prím esetén igaz a Fermat-tétel I. esete.

Sophie noha teljes egészében nem járt sikerrel a nagy Fermat-sejtés bizonyításával, érdemei elvitathatatlanok. Elsőként próbálkozott nem eseti jelleggel közelíteni a problémához, hanem tervszerűen igazolni azt. Közel kétszáz évvel később Leonard Adleman és Roger Heath-Brown az ő módszerére alapozva bizonyították, hogy a Fermat-tétel I. esete végtelen sok prímre fennáll.

Sophie prímjei

Általában véve is a tudomány, azon belül a matematika fejlődésének egyik legalapvetőbb vonása, hogy egy-egy sikertelen vagy sikeres próbálkozás gyakran eredményez melléktermékként olyan új felismeréseket, módszereket, ötleteket, melyek önmagukban vagy más területeken is érdekessé, fontossá válhatnak. Kiváló példa erre Sophie munkássága is, hiszen az általa felfedezett prímek a modern világunk egyik alapkövének számító kriptográfiában fontos szerepet töltenek be.

Emlékeztetőül, Sophie Germain prímeknek hívjuk az olyan p prímszámokat, melyekre igaz az, hogy a kétszeresüknél 1-gyel nagyobb szám, azaz a 2p+1 is prím. Ilyenek például a 2 vagy a 3, mert 2·2+1=5, illetve a 2·3+1=7 is prímek, de például a 7 vagy a 13 már nem, mivel 2·7+1=15, illetve 2·13+1=27 nem prím. A Germain-prímekkel kapcsolatban máig nyitott kérdés, hogy végtelen sok van-e belőlük. A probléma szoros kapcsolatban áll a matematika egy másik híres még megválaszolatlan rejtélyével, az ikerprím sejtéssel, mely azzal kapcsolatos, hogy végtelen sok olyan prímpár van-e, melyek között a különbség épp 2 (pl. 3 és 5, 5 és 7, 11 és 13 stb.)

A Germain-prímeknek számos érdekes számelméleti tulajdonságuk van. Ilyen például, hogy egy 3-nál nagyobb p esetén, ha p Germain-prím, akkor 3-mal osztva mindenképp 2 maradékot kell adnia. Hárommal ugyebár nyilván nem lehet osztható, mivel 3-nál nagyobb és prím, ha viszont 1 maradékot adna, akkor a q=2p+1 osztható lenne 3-mal, ami ellentmondana q prím voltának.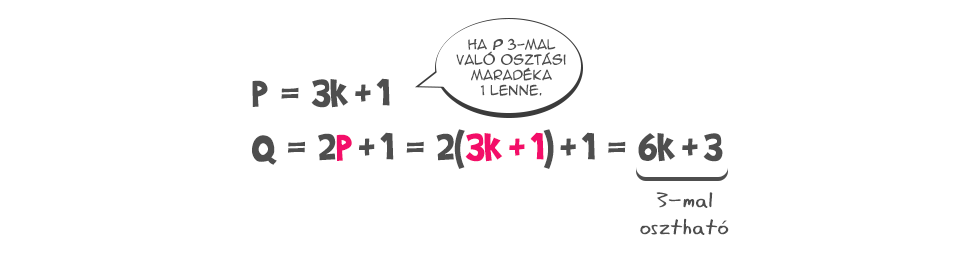Egy másik érdekesség, ha egy Germain-prím 4-gyel osztva 3 maradékot ad, azaz p=4k+3 alakú, akkor a 2p+1 alakú párja 8k+7 alakú lesz, és egyben osztója a 2^p-1 Mersenne számnak (ezek a 2 hatványoknál 1-gyel kisebb számok: 0, 1, 3, 7, 15, 31 stb.). Euler korábban egyébként igazolta, hogy ez a tulajdonság feltétele is annak, hogy egy prímindexű Mersenne-szám (azaz a 2^p-1) összetett szám lehessen.

A Germain-prímek kapcsán említést kell tennünk a prímek egy másik nevezetes csoportjáról is, az úgynevezett biztonságos prímekről. Ezek olyan prímek, amikre az igaz, hogy a náluk 1-gyel kisebb szám fele is prím. Lényegében ez épp a Germain-prímeknél látott szabályszerűség fordítottja. Fontos különbség viszont, hogy a kiindulópontunk és a következtetés iránya is más, így a két halmaz is eltér. Egy Germain-prímnek viszont mindig van egy biztonságos prímpárja és viszont:A fentiek egyik következménye, hogy ha kiindulunk egy Germain-prímből, például a 2-ből, és megalkotunk egy olyan láncot, melyben a soron következő tag mindig az előző tag kétszeresénél 1-gyel nagyobb, és ezt a metódust csak addig folytatjuk, amíg prímszámot kapunk egy adott lépésben, akkor e láncban az utolsó elem kivételével mindegyik Germain-prím, illetve az első kivételével mindegyik biztonságos prím lesz. Más szóval, a konstrukció – amit a szakirodalom 1-es típusú Cunningham láncnak hív – tetszőleges Germain-prímből elindítható, és mindig egy biztonságos prímnél akad el.A Germain-prím és biztonságos prím párok, ahogyan bizonyos prímpárok általában, fontos szerepet töltenek be a kriptográfiában, persze sokkal nagyobb nagyságrendben, a gyakorlatban alkalmazott prímek 1 846 389 521 368 + 11⁶⁰⁰-nál is nagyobbak.

A Sophie Germain-prímek a kriptográfiai alkalmazások mellett használhatók például pszeudo-véletlen számok előállítására is. Ez olyan számok sorozatát jelenti, melyben az egymást követő tagok statisztikai értelemben véletlennek tekinthetők. Vegyünk egy olyan p Germain-prímet, amire igaz, hogy 20-szal osztva 3, 9 vagy 11 maradékot ad, azaz például a 3-at vagy a 11-et. Ekkor ugye q=2p+1 is prím, vegyük q reciprokát tizedestört alakban. Igazolható, hogy ebben az alakban az 1/q első q-1 darab tizedesjegye egy pszeudo-véletlen sorozatnak tekinthető. (Mivel 1/q racionális szám, csak az első q-1 tizedesjegyet vizsgálhatjuk érdemben, hisz ezt követően szabályosan ismétlődnek már a számjegyek.)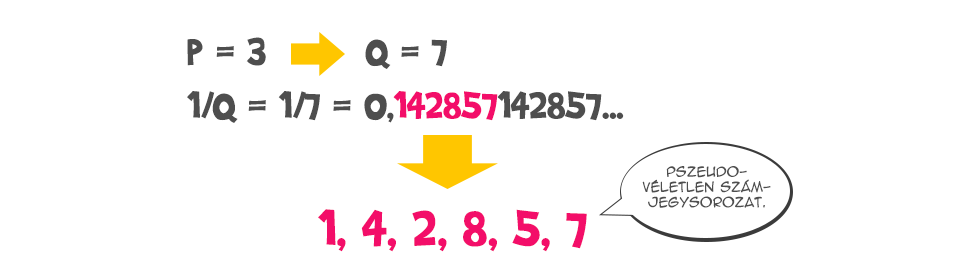

Utolsó évei

Kalandos matematikai pályafutása után és mellett, életének alkonyán Sophie Germain a filozófia felé fordult. Halála után jelent meg egy esszéje, mely azt taglalta, hogy az ember minden cselekedetében ott van az intellektuális folyamat, az emberi szellem intellektuális analógiák felismerésével fedezi fel az univerzum csodáit.

Élete utolsó két évében is sokat foglalkozott még számelmélettel és a rezgésekkel kapcsolatos munkáival is. Egyes források szerint Gauss nem sokkal Sophie halála előtt elérte a Göttingeni Egyetemen, hogy a nő díszdoktori címet kaphasson, más források szerint viszont épp, hogy nem volt elég célratörő e kérdésben. Akárhogy is, Sophie sajnos már nem élhette meg a cím neki ítélését, 1829-ben mellrákot diagnosztizáltak nála, ami két évvel később el is vitte. (Érdekesség, hogy halálának éve, 1831 is prím, bár igaz, nem Germain-prím.)

Jól mutatja korának megbecsülését iránta, hogy a halotti bizonyítványában a foglalkozásához nem a matematikus vagy a tudós megnevezés, hanem az „ingatlantulajdonos” bejegyzés került. Az utókor viszont lerótta tiszteletét Sophie előtt. Nevét halálának helyszínén, a párizsi rue de Savoie 13. szám alatti épületen, emléktábla őrzi. Párizsban utcát és iskolát is neveztek el róla, az utcában egy kisebb, szintén a nevét viselő hotel is található, szobra pedig a Sophie Germain iskola udvarán áll.

Források:

https://mathshistory.st-andrews.ac.uk/Biographies/Germain/

https://hu.wikipedia.org/wiki/Sophie_Germain

https://artofproblemsolving.com/wiki/index.php/Sophie_Germain_Identity?srsltid=AfmBOoo7-kcJwkXslJ7Kmzj5yq-5Q-A9A65LZYtdQ7LuX0WThU4bfYxd

https://en.wikipedia.org/wiki/Sophie_Germain%27s_identity

https://www.britannica.com/biography/Sophie-Germain

https://en.wikipedia.org/wiki/Safe_and_Sophie_Germain_primes

https://www.termvil.hu/2021/02/23/tudosno-a-matematikaban/

https://hu.wikipedia.org/wiki/Pr%C3%ADmsz%C3%A1mok_list%C3%A1ja

https://ematlap.hu/tudomany-tortenet-2018-03/647-wiles-es-az-iwasawa-elmelet

Simon Singh – A nagy Fermat-sejtés (Park Könyvkiadó 2017)

https://mathwomen.agnesscott.org/women/germain-FLT/SGandFLT.htm

https://www.theoremoftheday.org/Binomial/GermainId/TotDGermainIdentity.pdf

https://mathshistory.st-andrews.ac.uk/HistTopics/Fermat's_last_theorem/

https://www.math.mcgill.ca/darmon/courses/12-13/nt/projects/Colleen-Alkalay-Houlihan.pdf

https://www.isibang.ac.in/~sury/afsant.pdf

https://mathwomen.agnesscott.org/women/germain.htm