Minden idők egyik legnagyobb matematikusa, Leonhard Euler már fiatalabb korában érdeklődött Pierre de Fermat azon tétele iránt, miszerint egy egész szám valamely prím kitevőjű hatványa az adott prímmel osztva mindig épp annyi maradékot ad, mint amennyit maga a szám. Azaz például a 10³, ami 1000, ugyanúgy 1 maradékot ad 3-mal osztva, mint a 10, hiszen 10=3·3+1 és 1000=333·3+1. Ezt nevezzük „kis" Fermat-tételnek. (Létezik „nagy” Fermat-tétel is, mely viszont egészen más tészta, ennek történetéről Simon Singh írt A nagy Fermat-sejtés (Park Könyvkiadó, 2004.), címmel remek könyvet.)

Euler egyéb elfoglaltságai miatt csak nagyjából két évtizeddel később tért vissza a témához. Kibővítette Fermat eredeti állítását, és a később Euler-Fermat-tétel néven elhíresült tétel levezetése során bevezette a róla elnevezett j függvényt. Noha ő maga még nem függvényként tekintett rá, és nem is így jelölte (hanem p-vel, csak később Gauss vezette be a fN jelölést, amiből a j lett idővel), néhány fontos tulajdonságát, mint például a megadás módja prímhatványok esetén vagy a gyenge multiplikativitás, már ő maga levezette.

A lényegre térve, az Euler-Fermat-tétel egy pontján meg kell tudnunk adni, hogy egy adott pozitív egész számhoz hány relatív prím van a nála nem nagyobb pozitív egészek körében. (Két szám akkor relatív prím, ha nincs 1-nél nagyobb közös osztójuk.) Euler j függvénye pontosan erre a kérdésre adott választ.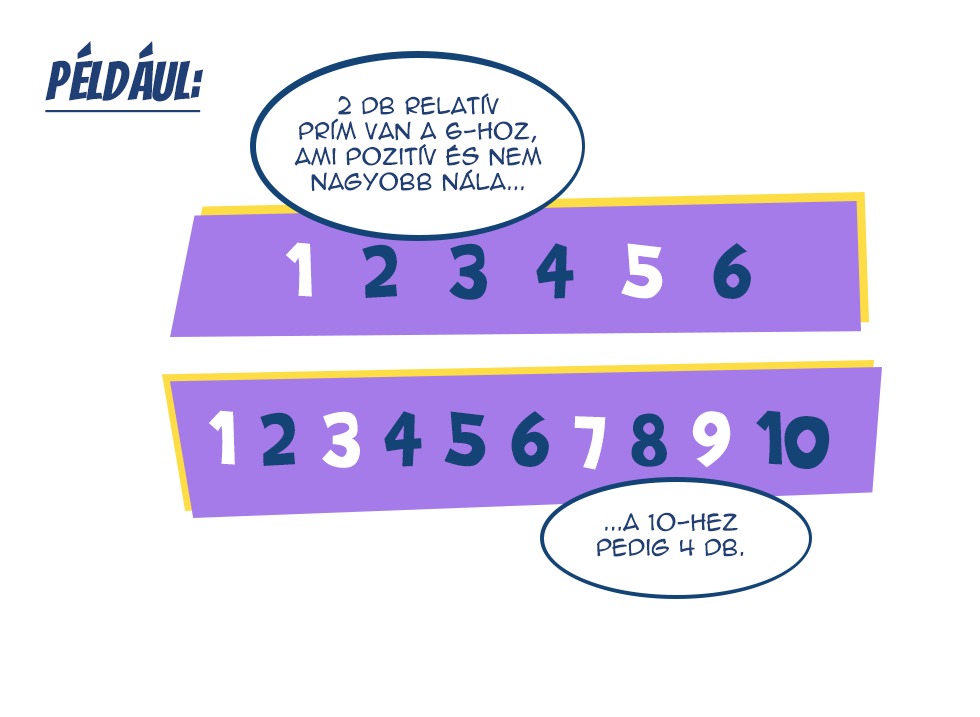

Az 1 és a prímek esete

Kezdjük a legegyszerűbb esettel, az 1-gyel. Hozzá relatív prím a nála nem nagyobb pozitív egészek között csak saját maga, tehát 1 db ilyen szám van, azaz: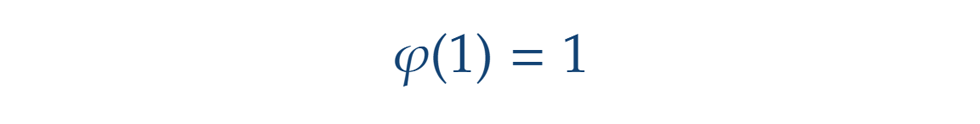

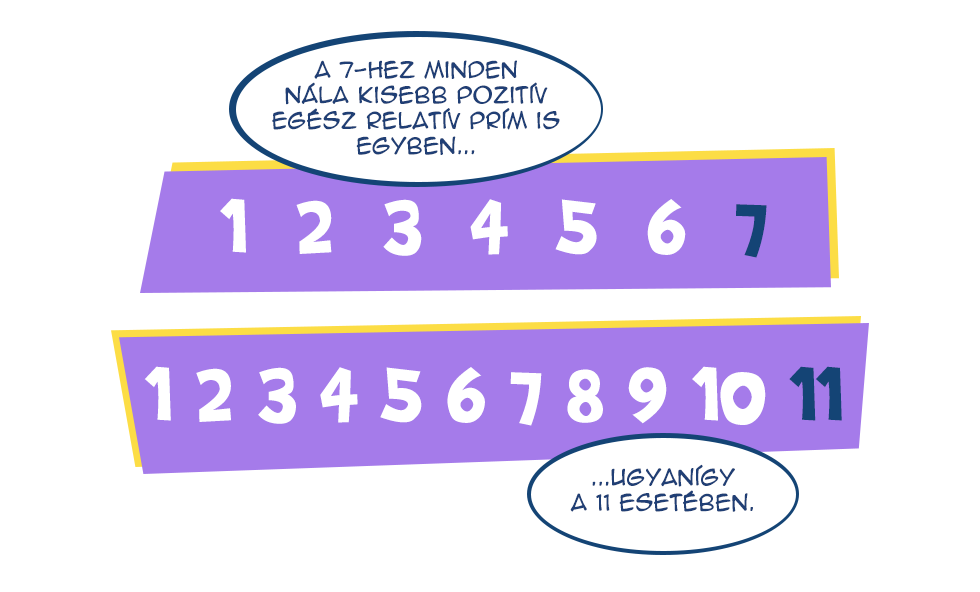
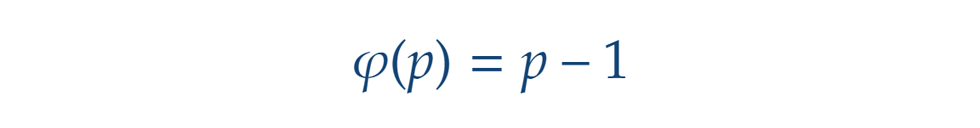
Számelméleti szempontból a legegyszerűbb esetek listáján a következő helyet a prímszámok foglalják el. Ezek eleve olyan számok, amik csak 1-gyel és saját magukkal oszthatók. Így viszont minden náluk kisebb pozitív egész, relatív prím lesz hozzájuk, hiszen – mivel kisebbek, egyfelől az adott prímmel biztosan nem oszthatók, a prímünk viszont mással nem nagyon, így mi más lehetne a legnagyobb közös osztójuk, mint az 1.

Általánosan megfogalmazva, egy p prím esetén a nála nem nagyobb, hozzá relatív prímek száma a pozitív számok körében p-1:

Prímhatványok

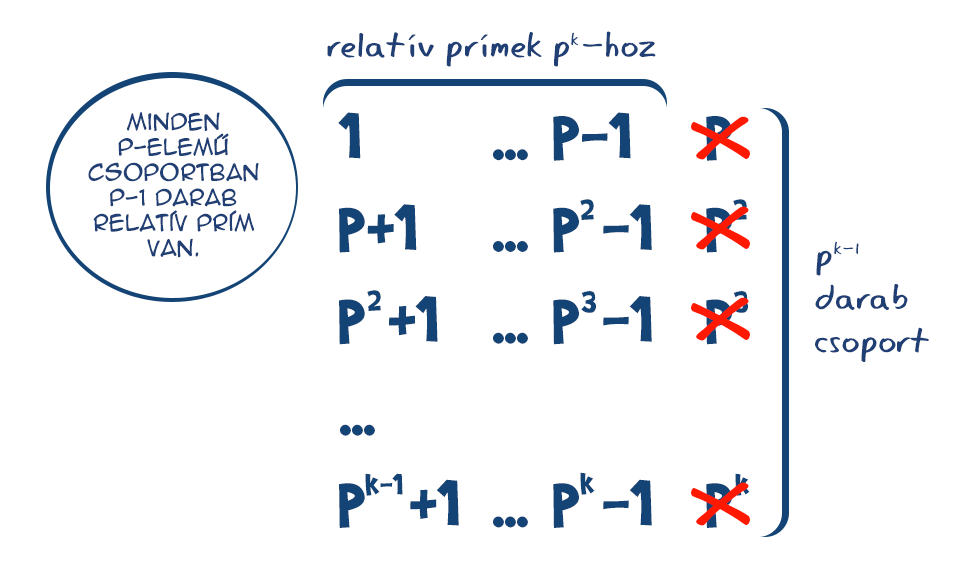
Menjünk tovább. Lássuk a prímek hatványait, azaz az olyan számokat, mint a 4, 8, 9, 16 stb. Egy prímhatványnak pontosan azokkal a számokkal lesz 1-nél nagyobb közös osztója, amik oszthatók az alapjául szolgáló prímmel, azaz melyek prímtényezős felbontásában szerepel ez a prímszám.

Vegyük például a 8-at. Ez 2³, tehát a 2-vel osztható, azaz a páros számokkal biztosan nem lesz relatív prím. Ezek a számok épp kettesével jönnek, így tulajdonképpen minden második számot kapásból ki is húzhatjuk a listáról.

Lássunk egy másik példát. A 27 a 3 harmadik hatványa. Nem alkothat tehát relatív prím párt egyik 3-mal osztható számmal sem. A többi nála kisebbel viszont igen, mert azok tuti nem oszthatók 3-mal, míg ő csak a 3 hatványaival az. A 3-mal osztható számok persze hármasával jönnek, azaz ezúttal minden harmadik számot kell átugranunk. Így a keresett relatív prímek száma 27-9 = 27-27/3 = 18 lesz.

Kezd kirajzolódni egy minta. A 2 hatványa esetén minden második, a 3 hatványa esetén minden harmadik számot kellett kihagynunk. A sort folytathatnánk, egy 5-hatvány esetén például minden ötödiket kellene:

Tehát, ha felsoroljuk az egész számokat 1-től indulva az adott p^k prímhatványig, és felosztjuk a sort akkora csoportokra, amik darabszáma az adott prímmel (p) egyezik meg, akkor minden ilyen csoportból egy, a p-vel osztható, kivételével az összes többi relatív prím lesz p^k-hoz.

A csoportok száma épp a p^k szám p-ed része, azaz p^k/p = p^k-1, így összegezve, egy p^k prímhatvány esetén a nála nem nagyobb és hozzá relatív prímek száma:

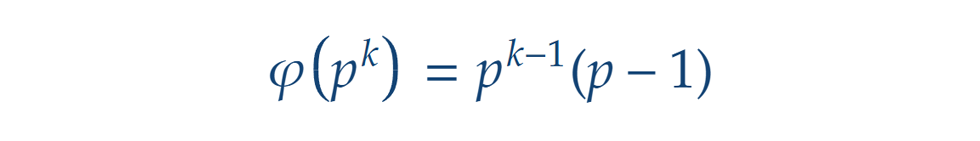
Gyenge multiplikativitás

Szusszanjunk egy kicsit, és térjünk ki az Euler-féle j függvény úgynevezett gyenge multiplikativitására. Ez azt jelenti, hogy ha szeretnénk megtudni a j értékét két relatív prímszám, pl. n és m szorzata esetén, akkor elég összeszoroznunk j(n)-t és j(m)-et. Például, a korábbiak alapján j(6)=2 és j(5)=4, amiből j(30)=2·4=8. És valóban: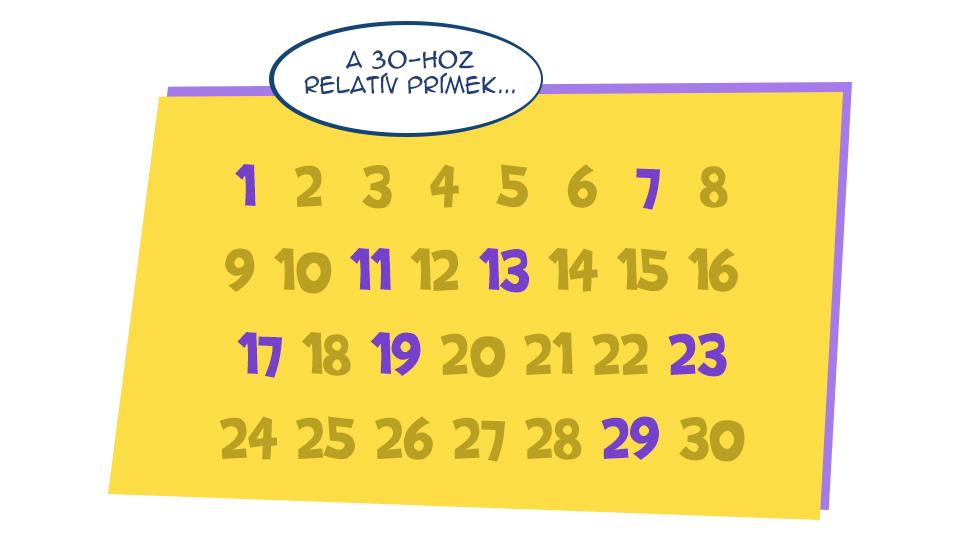

Rendezzük el az 1-30 közti egész számokat 5 sorba és 6 oszlopba (vagy fordítva). Ekkor a 6-hoz relatív prímek az 1-es és az 5-ös oszlopában találhatók, a táblázat többi száma biztosan nem jó.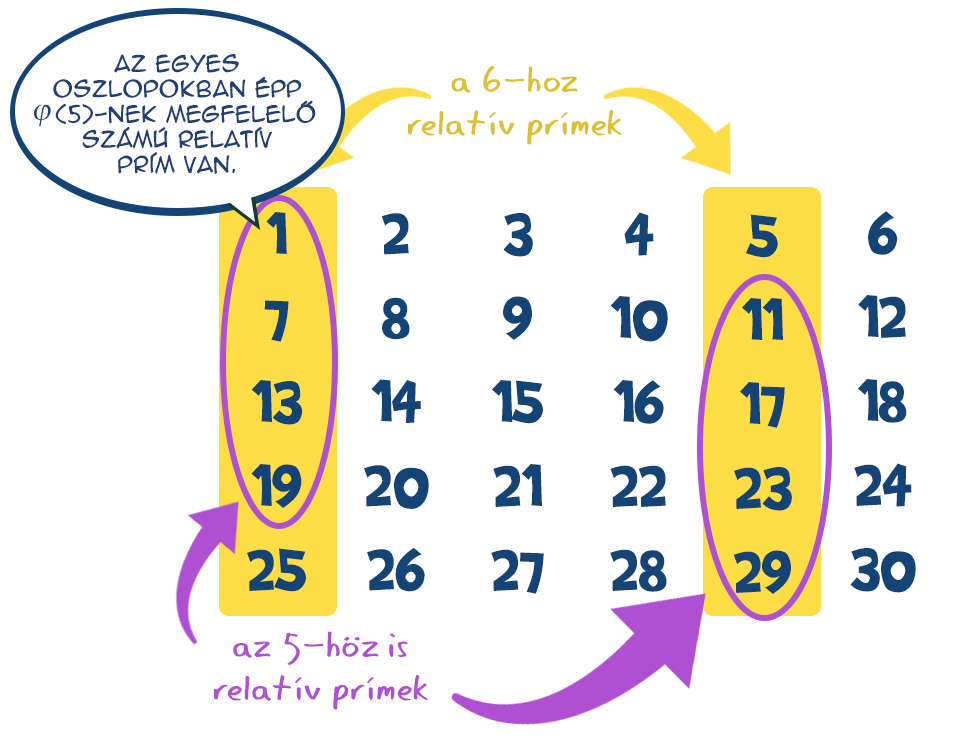

Ugyanez történik az ötödik oszlopban is, annyi különbséggel, hogy a maradékok más sorrendben jönnek elő (a csere: 5 marad, 11 helyett 1, 17 helyett 2, 23 helyett 3, 29 helyett 4). Összességében tehát annyiszor j(5) db relatív prím van a 30-hoz, ahány színezett oszlop van, azaz ahány relatív prím van a 6-hoz, ami viszont j(6) darabot jelent. Más szóval: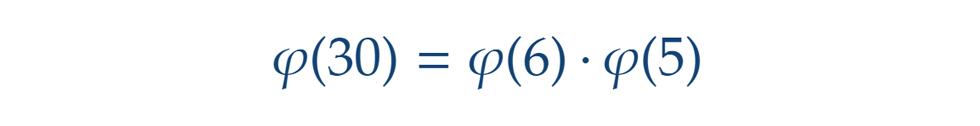

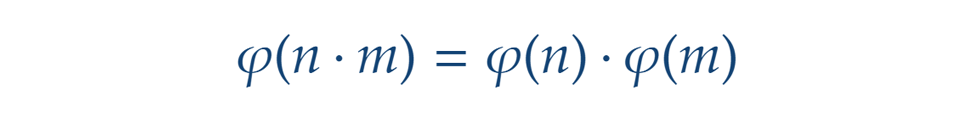
Ugyanez általánosan is elképzelhető egy n-sorú m-oszlopú táblázattal, ha n és m relatív prímek. Először is j(m) darab oszlop lesz, ami az m-hez relatív prímeket tartalmazza. Belátható, hogy az egy oszlopban szereplő számok mindig teljes maradékrendszert fognak alkotni modulo n, ezek között pedig definíció szerint j(n) darab olyan szám lesz, ami n-hez is relatív prím. Így összességében:

„Erős” multiplikativitás?

Már csak egy tisztázandó kérdés lehet bennünk, mi a gond azzal, ha a számok nem relatív prímek? Például 6 és 4 esetén a 6-hoz relatív prímek ugyanúgy az első és ötödik oszlopban találhatók, de nem teljesül, hogy oszlopokon belül a 4-gyel vett osztási maradékok mind különböznének.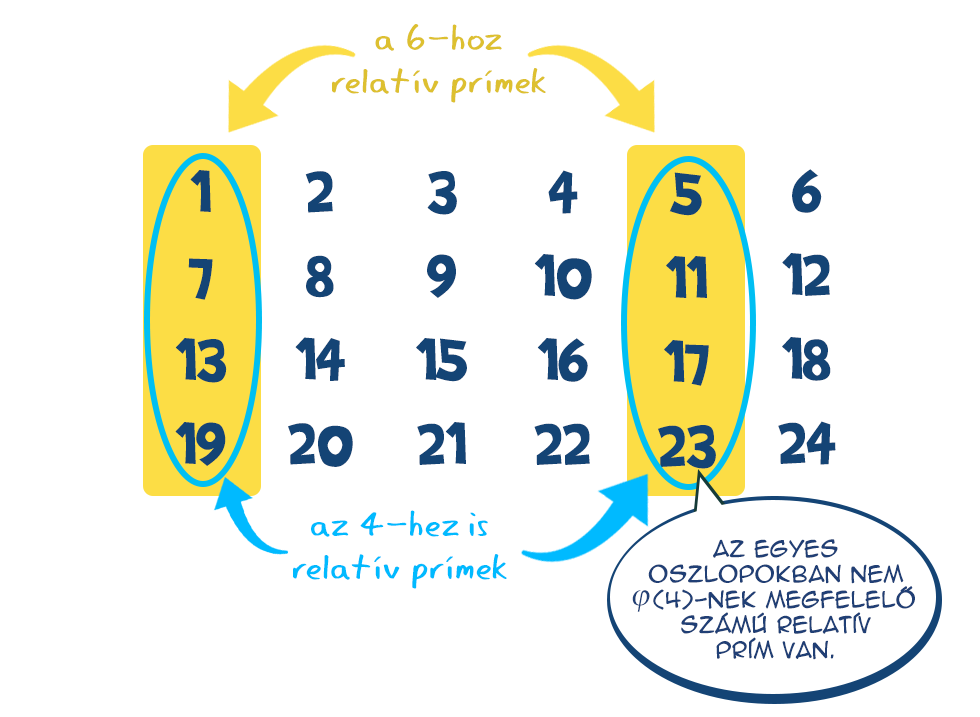

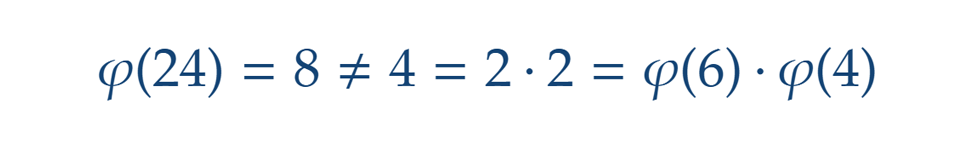
Itt például a színezett oszlopok minden tagja relatív prím a 4-hez, és a 24-hez is, azaz

Szép dolog mindez, de hogy kapcsolódik a továbbiakhoz? A válasz, hogy erősen megkönnyíti j(n) meghatározását az általános esetben.

Összetett számok

A gyenge multiplikativitással a kezünkben már nem okoz gondot j(n) megadása összetett (nem feltétlenül prímhatvány) számok esetén sem. A számelmélet alaptétele szerint az összetett számok prímhatványok szorzatára bonthatók, ráadásul egyértelműen, leszámítva a szorzat tényezőinek sorrendjét. Például 360 = 2³·3²·5. A felbontásában szereplő prímhatványokra már ki tudjuk számolni j értékét a korábbiak szerint: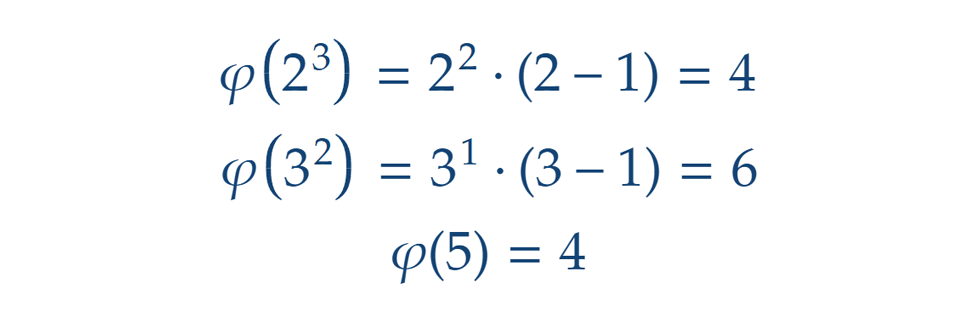

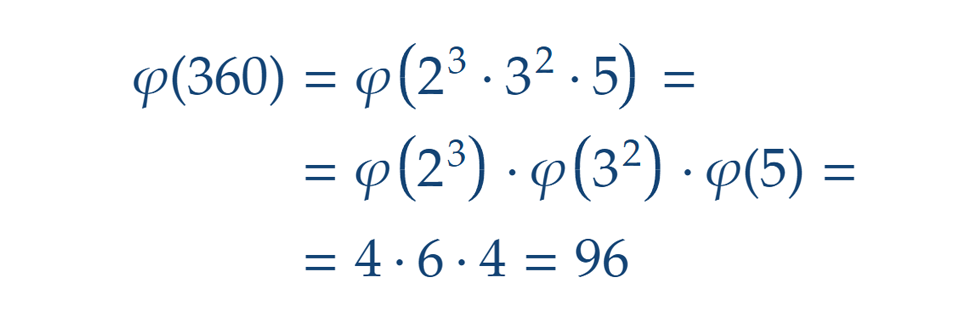
E prímhatványok közül viszont bármelyik kettő biztosan relatív prím, hiszen különböző prímek hatványai. (Az egyik osztható 2-vel, de a többiek nem. Az egyik osztható 3-mal, de a többi nem. Az egyik osztható 5-tel, de a többi nem.) Így a gyenge multiplikatív tulajdonságnak köszönhetően

Jegyezzük meg azt is, hogy a fenti gondolatmenet triviálisan igaz, ha a szám pusztán egyetlen prím valamely hatványa, beleértve akár a nulladik hatványt is. Persze utóbbi esetben kihasználjuk, hogy j(1)=1.

Végezetül fogalmazzuk meg a fentieket általánosan. Legyen egy n pozitív egész szám prímtényezős felbontása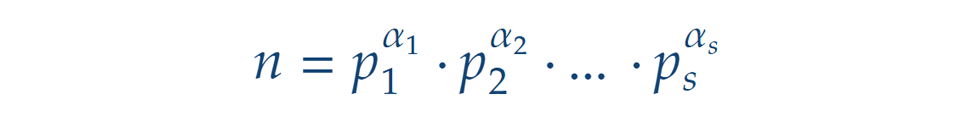

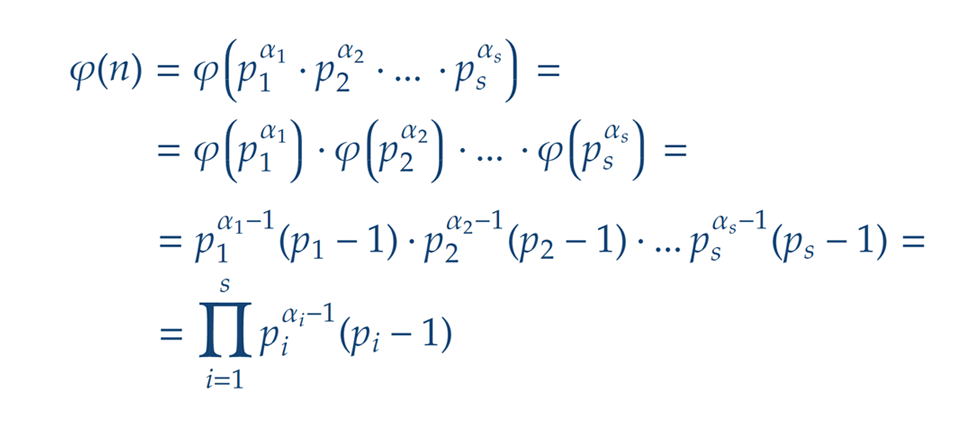
ahol p_i-k különböző prímek, a_i-k pedig nemnegatív egész számok. Ekkor az n-hez nála nem nagyobb relatív prímek száma megkapható a

képlettel.

Forrás:

Megyesi László: Bevezetés a számelméletbe (Polygon Jegyzettár 1997)

https://maa.org/press/periodicals/convergence/math-origins-the-totient-function