Egy pozitív egész szám osztóinak számát meghatározhatjuk azok konkrét felírása nélkül is a szám prímtényezős felbontása ismeretében. Ahhoz, hogy lássuk, ez egész pontosan hogyan is történik, vizsgáljuk meg először a legegyszerűbb eseteket. Mindenekelőtt, az 1-nek egyetlen pozitív osztója van, saját maga, a prímszámoknak pedig – a prím tulajdonság értelmében – két-két darab, az 1, és önmaguk.

A számok felépítését tekintve a következő szintet a prímek hatványai jelentik. A válaszadás itt ütközik először nehézségekbe, de némi töprengés után ezt az akadályt is magunk mögött tudhatjuk. Ebben az esetben a legfontosabb, amit látnunk kell, hogy egy prímhatvány mindig csak az alapjául szolgáló prím hatványaival osztható, és azok közül is csak azokkal, melyek kitevője nem haladja meg az eredeti prímhatvány kitevőjét. Persze, mivel csak pozitív osztókra vadászunk, alsó korlát is van, a legkisebb szóba jöhető kitevő a nulla.

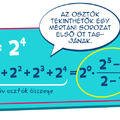
Például a 16 (ami 2⁴) pozitív osztói az 1, 2, 4, 8, 16, ami mind 2 hatvány:Ezeket viszont könnyű összeszámolni, a 2⁴-nek 5 darab pozitív osztója lesz, ami a 2 kitevőjénél épp 1-gyel több. A jelenség magyarázata, hogy egy osztó esetén a 2 kitevőjének 0-tól 4-ig bármilyen egész számot választhatunk.

Általánosságban ugyanez a helyzet, azaz ha az adott prímhatványunk p^k alakú, akkor az osztói is ilyen alakúak kell, legyenek, ezek kitevői pedig 0-tól k-ig bármilyen egészek lehetnek, ami így összesen k+1 darab lehetőséget jelent, tehát p^k-nak k+1 pozitív osztója lesz.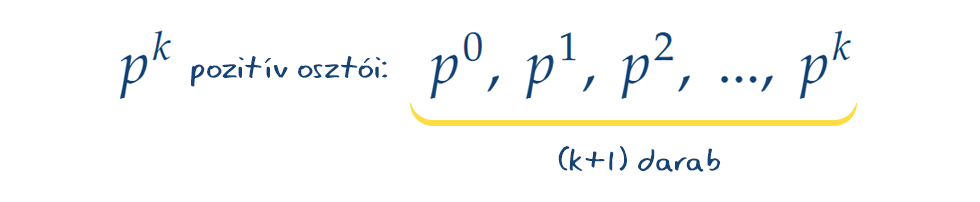Lépjünk még egy szinttel feljebb, lássuk az olyan összetett számokat, melyek nem feltétlenül egyetlen prím hatványai. A számelmélet alaptétele értelmében ezek egyértelmű módon prímhatványok szorzatára bonthatók. Amikor egy összetett szám osztóit összeállítjuk, a felbontásában szereplő prímek hatványaiból válogathatunk úgy, hogy az ott szereplő hatványkitevőket nem lépjük túl, de továbbra is megengedett, hogy a prímeknek a nulladik hatványait válasszuk.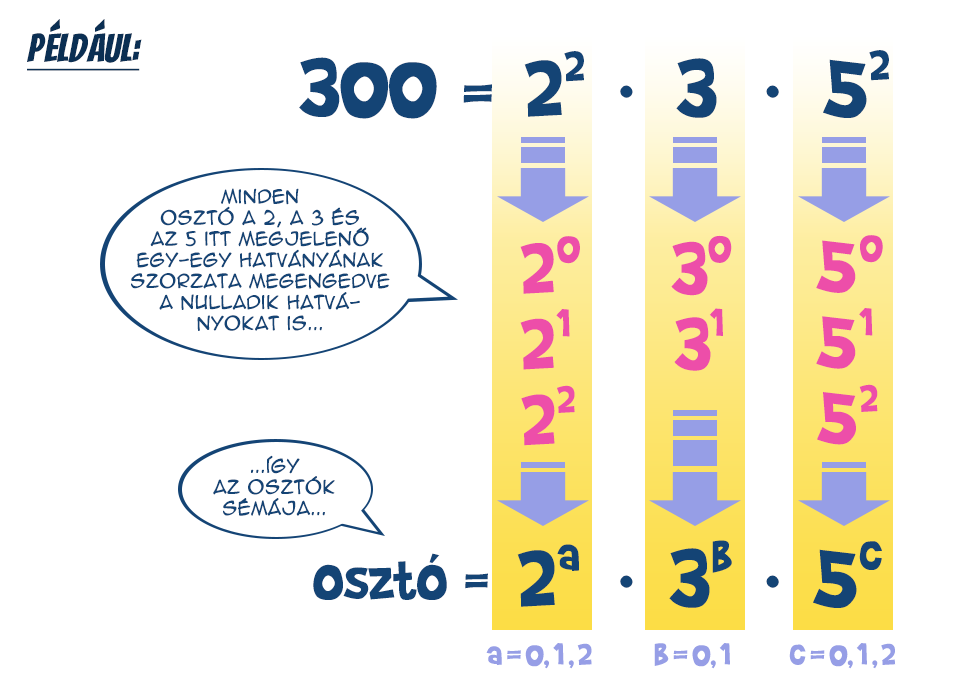Ily módon a felbontás mindegyik prímhatványa esetén az ő kitevőjénél, a nulladik hatvány miatt, 1-gyel több lehetőségünk lesz a választáskor. A különböző prímek hatványai pedig tetszőlegesen kombinálhatók, így összesen annyi osztót tudunk megalkotni, amennyi a kitevők 1-gyel növelt értékeinek szorzata.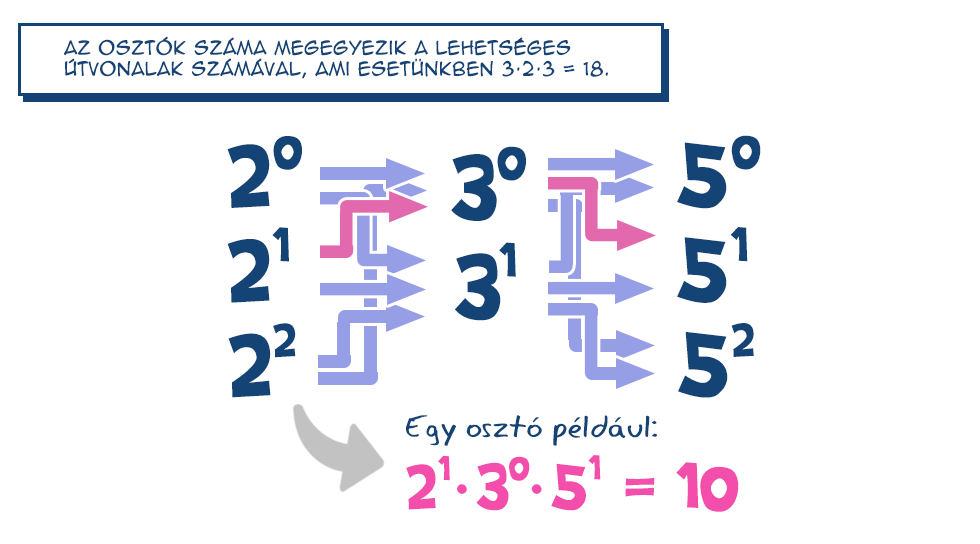Általánosan, ha egy n pozitív egész szám prímtényezős felbontása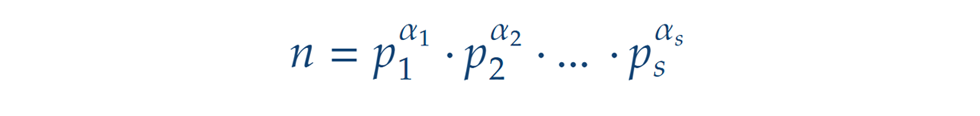ahol minden a_i nemnegatív egész, akkor n pozitív osztóinak száma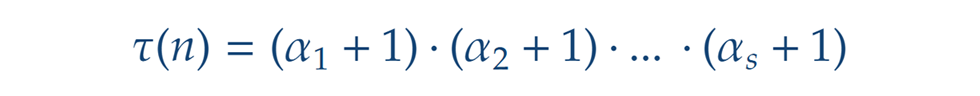

azaz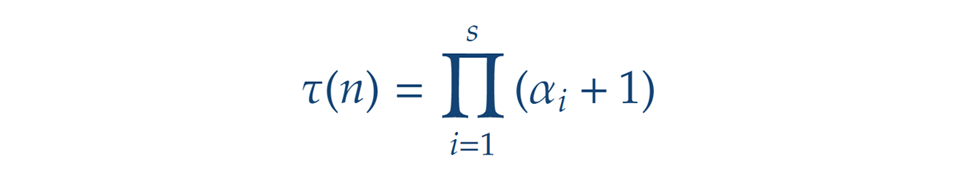Az n pozitív osztóinak számát a t(n) jelöli, ami mellett gyakori még a d(n) jelölés is (divisor = osztó).

A fentiekben egy úgynevezett számelméleti függvényt vezettünk be, ami egy olyan függvényt jelent, melynek értelmezési tartománya a természetes számok halmaza, de egyúttal számelméleti tartalommal is bír.

Gyenge multiplikativitás

Az osztók számának meghatározása az általános esetben lényegében úgy történt, hogy az n szám felbontásában szereplő prímhatványok osztóinak számát szoroztuk össze. Például a 300 esetén a 2²-nak három, a 3-nak kettő, az 5²-nak pedig szintén három pozitív osztója volt, így a 300-nak 3·2·3=18 darab.

Vajon ez a tulajdonság tetszőleges felbontás esetén is működne? Vagy szükséges, hogy prímhatványok szorzatára bontsuk fel az adott számot? A válasz igazából mindkét kérdésre a nem lesz, utóbbinál ugyanis egy gyengébb feltétel is elég, ugyanakkor korántsem igaz, hogy bármilyen felbontás megfelelő lenne.

Maradva a 300 példájánál, például a 3·100-as felbontás ugyanúgy jó, mivel a 3-nak két osztója van, a 100-nak pedig (a prímfelbontása alapján) hat darab, a 3·6 pedig épp 18. Nem működik ugyanakkor a dolog például az 6·50-re, hisz a 6-nak négy, az 50-nek hat pozitív osztója van, melyek szorzata 24, nem pedig 18.

Mitől függ, hogy egy felbontás jó vagy sem? Mi a baj a 6·50-es felbontással? Utóbbi esetén alapvetően az a probléma, hogy van „átfedés” a 6 és az 50 prímfelbontásában szereplő prímek között (azaz lényegében a 6 és 50 1-nél nagyobb osztói között), így a 300 bizonyos osztói többféleképpen is előállnak a 6 és az 50 prímtényezőiből.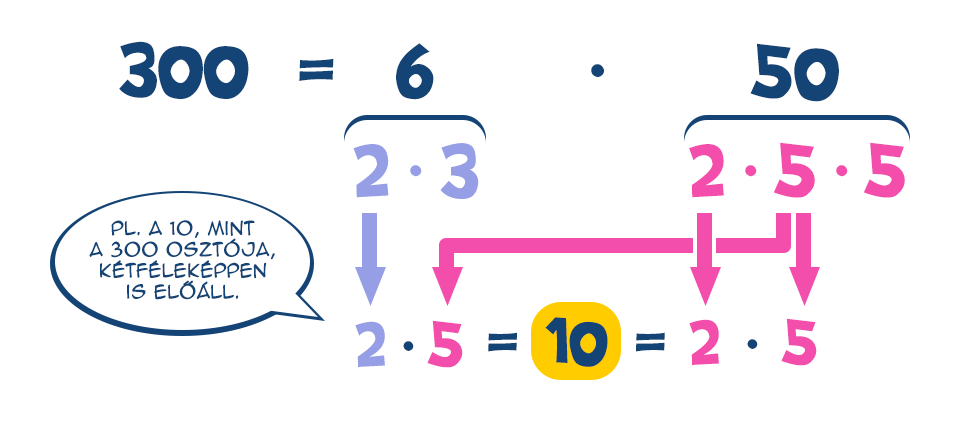Ilyesmi a 3·100-as felbontás esetén viszont nem fenyeget, mivel a 3 osztói csak az 1 és a 3, de a 100 nem osztható 3-mal, így ez esetben minden osztó pontosan egyféleképpen kapható meg.

Az olyan számokat, melyeknek nincs közös prímtényező a felbontásukban, relatív prímeknek nevezzük. (Más megközelítésben, az ilyen számok legnagyobb közös osztója 1.) Ez lesz az a tulajdonság, aminek (páronkénti) teljesülését megköveteljük az adott n szám szorzattá alakításában szereplő tényezőktől ahhoz, hogy az n osztóinak száma előállhasson az egyes tényezők osztószámainak szorzataként. Precízebben, ha n előáll n=a·b alakban, ahol a és b relatív prímek, akkor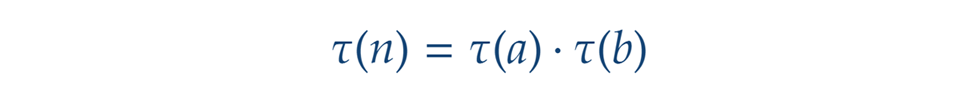Még egy apróság. Ha n-t n=1·n-ként bontjuk fel, akkor a fentiek alapján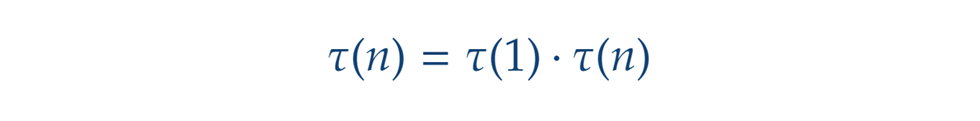amiből következik, hogy a pozitív osztók számát megadó függvénynek az 1-hez az 1-et kell rendelnie, ami esetünkben persze nyilvánvalóan teljesül.

A fenti két tulajdonságot együttesen teljesítő számelméleti függvényeket gyengén multiplikatívnak nevezzük. (A „sima” multiplikatív tulajdonság azt jelentené, hogy a relatív prím megkötés nélkül is igaz a fenti két összefüggés.) A legismertebb számelméleti függvények mind rendelkeznek majd ezzel a tulajdonsággal, ahogy ezt a későbbiekben látni is fogjuk.

Nem pozitív osztók

Végezetül térjünk ki arra a tényre is, hogy egy egész számnak persze negatív osztói is lehetnek. Mivel azonban, ha egy n egész számnak osztója az a egész szám, akkor annak ellentettje, azaz (-a) is az, a negatív és pozitív osztók párba állíthatók, így n-nek épp t(n) darab negatív osztója is lesz, vagyis az osztóinak száma összesen 2·t(n).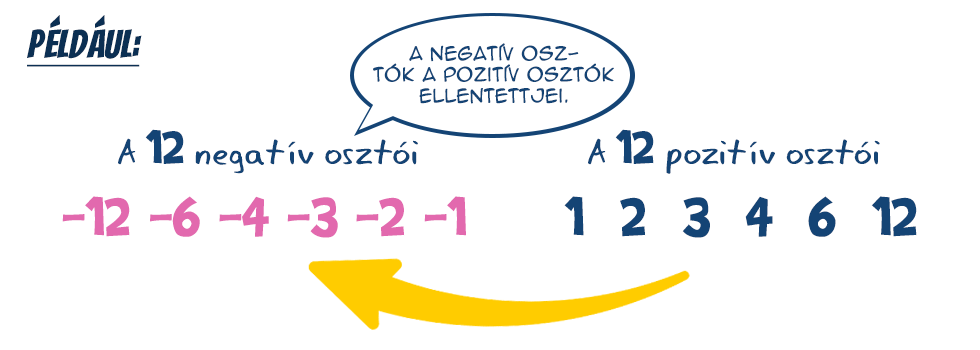A nulla kivételével a nullával, mint osztóval nem kell számolnunk, mert a nulla csak saját magának lehet osztója, a nulla osztóinak száma viszont végtelen, mert minden egész szám osztja. Például 3 | 0, hiszen létezik olyan egész szám, hogy 3-mal megszorozva 0-át kapjunk, mégpedig épp a 0.

Forrás:

Megyesi László: Bevezetés a számelméletbe (Polygon Jegyzettár 1997)