Hasonlóan ahhoz, ahogyan a természetes számok pozitív osztóinak számát meghatároztuk, megkaphatjuk ezen osztók összegét is az adott természetes szám prímtényezőinek ismeretében. Így egy újabb számelméleti függvényt kapunk, ami sok hasonlóságot mutat az osztók számát megadó függvénnyel.

A félreértések elkerülése végett, ezúttal is, amíg mást nem mondunk, osztók alatt csak a pozitív osztókat értjük majd, illetve szintén jegyezzük meg, hogy mivel a 0-nak minden természetes szám osztója, ezek összege végtelen, tehát a folytatásban mindig csak pozitív egész számok osztóiról lesz szó.

Építőkockák

Kövessük a korábban már bevált utat, azaz kezdjük az egyszerűbb esetekkel. Az egyszerű esetek közül is a legegyszerűbb az 1-é, hisz az 1-nek egyetlen pozitív osztója van, önmaga, mely egy egytagú összeget jelent, ami természetesen 1. Az osztók összegére használt s(n) jelöléssel felírva s(1) = 1.

Lépjünk egy szinttel feljebb. Egy prímszám osztói az 1 és maga az adott prím, ezek összege tehát a prímnél 1-gyel nagyobb. Például a 3 osztói az 1 és a 3, ezek összege 4, vagy a 19 esetében 1+19=20. Általánosságban s(p) = p+1.

Prímhatványok

Eddig tiszta sor, nézzük a prímek hatványait. Láttuk, hogy egy prímhatvány osztói az adott prím legfeljebb ugyanakkora (nemnegatív egész) kitevőjű hatványai lehetnek, azaz például 2⁴ esetén a 2⁰, 2¹, 2², 2³, 2⁴. Ezek a számok ebben a sorrendben mindig a közvetlenül előttük állók 2-szeresei. Más szóval, tekinthetők egy olyan mértani sorozat első öt tagjának, melynek első tagja 2⁰, kvóciense pedig 2. Ekkor viszont ezek összege kiszámolható a mértani sorozat első n tagjának összegképlete alapján. Esetünkben az összeg 31.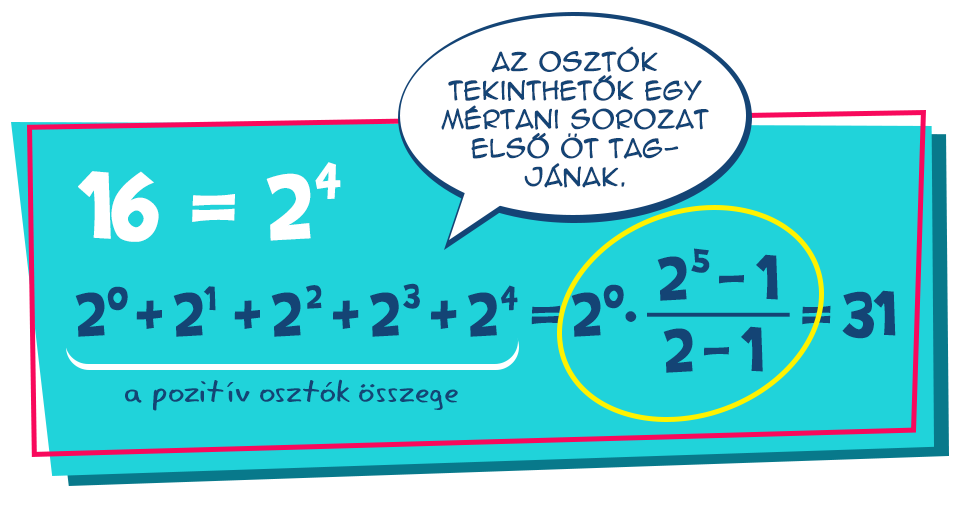Ez persze könnyen kiszámítható lett volna az osztók egyszerű összeadásával is, de nagyobb prímhatványok esetén a fenti módszer lényegesen hatékonyabb. Vajon működik a logikánk minden ilyen esetben?

Tekintsünk egy tetszőleges prímhatványt, p^k-t. Ennek osztói p⁰, p¹, p², …, p^k, melyek ugyanúgy egy mértani sorozat első k+1 tagjának tekinthetők, ahol az első tag p⁰, a kvóciens pedig maga a p. Így az első k+1 tag összege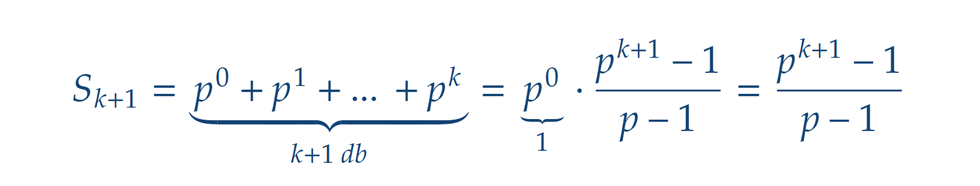Kijelenthető tehát, hogy a módszer mindegyik prímhatványra hasonlóan kifogástalanul működik.

Összetett számok

Elérkeztünk az általános esethez, jöhetnek a tetszőleges összetett számok, mint amilyen például a 72. Ennek prímfelbontása 2³·3², így osztói a következő alakúak: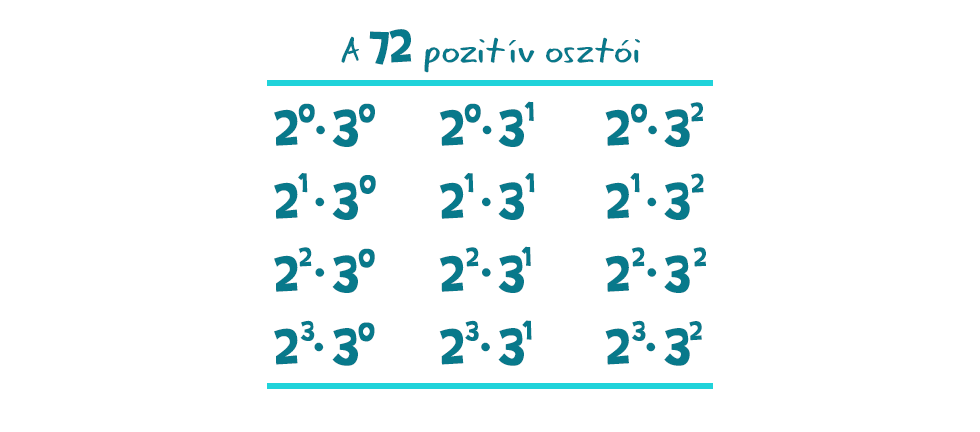E számok összegzése elsőre nehéznek tűnhet, de egy ügyes csoportosítással a probléma könnyen kezelhetővé válik. 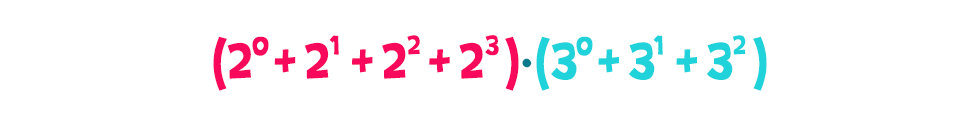Először is tekintsük az egy sorban szereplő osztókat, és emeljük ki mindenhol a közös tényezőt:Észrevehetjük, hogy minden zárójel ugyanazt a kifejezést takarja, így ez is kiemelhető egy második körben, így akifejezéshez jutunk. Na, de a két zárójel éppen a 2³ és a 3² osztóinak összege, azaz visszavezettük a problémát a prímhatványok esetére.

Sejtésünk ezek alapján, hogy egy összetett szám osztóinak összege a prímfelbontásában szereplő prímhatványok osztóösszegeinek szorzata lesz. A 72 esetén, hogy befejezzük a gondolatmenetet, ez a következő lesz: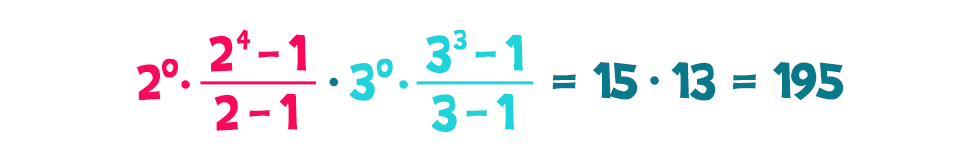Nézzünk egy másik példát is, melyben kettőnél több prímhatvány szerepel. Ilyen például a 60, ami 2²·3·5. Ennek osztóit nehezebb szépen, táblázatban elrendezni (igazából egy 3 dimenziós táblázatra lenne szükség), de azért nem lehetetlen:A táblázat nem olyan frappáns, de a csoportosítás hasonlóan működik. Mindenekelőtt tekinthetjük az 5 hatványai szerinti két csoportot:A zárójeleken belül újabb kiemelésekre van lehetőség a 3 hatványoknak köszönhetően: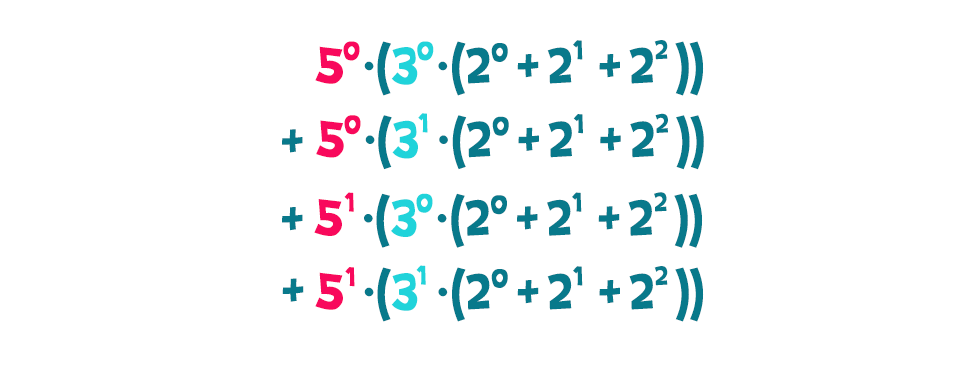Végül pedig a zárójelek kiemelésével ismét oda jutunk, hogy az osztók összege egyenlő a 60 felbontásában szereplő prímhatványok osztóösszegeinek szorzatával:A fentiekben látott csoportosító módszer az alapgondolata az általános eset bizonyításának is, az unalmas részleteket ezért elhanyagoljuk. Maga az állítás viszont így szól: ha egy pozitív szám prímtényezős felbontása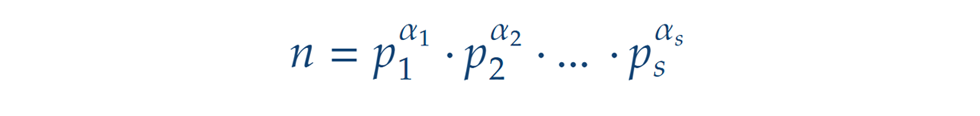akkor osztóinak összege kiszámolható az alábbi képlettel:

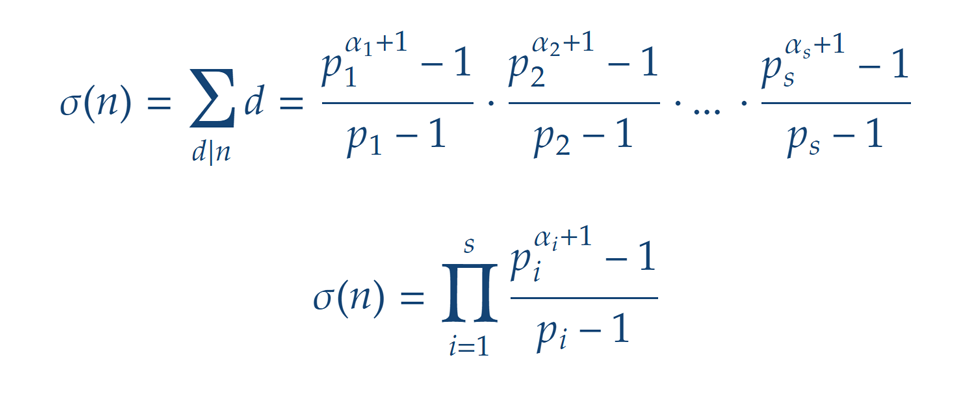
Gyenge multiplikativitás

Az osztók számát megadó számelméleti függvény egyik fontos tulajdonsága a gyenge multiplikativitás. Ott arról van szó, hogy ha az adott n természetes számot relatív prím tényezők szorzatára bontjuk, akkor az egyes tényezők osztószámainak szorzata épp az n osztószáma. A fentiek alapján joggal merülhet fel a kérdés, hogy vajon ugyanez elmondható-e az osztók összegét megadó függvényről is.

A korábbiakból következően annyi bizonyos, hogy prímtényezők esetén teljesül, hogy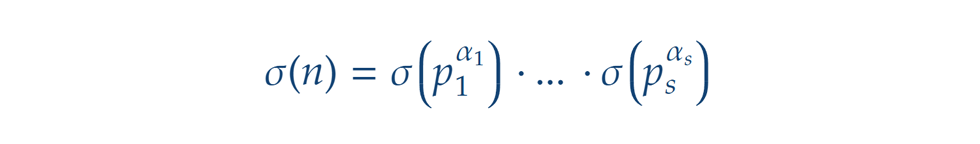ahol a különböző prímek hatványai természetesen páronként relatív prímek is egymáshoz. Vajon más felbontás is jó lehet? Térjünk vissza a 60 példájához. Ha a 60-ra úgy tekintünk, mint 4·15, ahol a 4 és a 15 relatív prímek (de nem feltétlen prímhatványok, akkor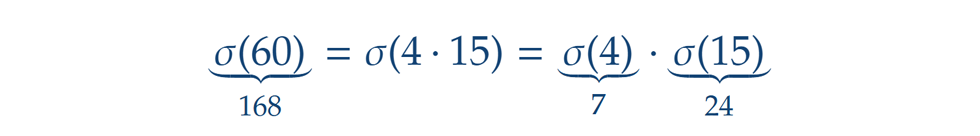valóban jó. Ugyanakkor, ha a 6·10 szorzatot vesszük alapul, már nem mondhatjuk el ugyanezt, persze a 6 és a 10 nem is relatív prímek: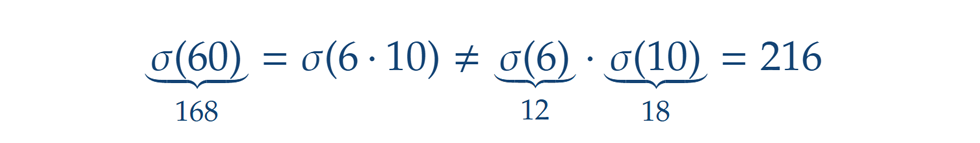A probléma lényegében ugyanaz, mint az osztók száma esetén volt, azaz, hogy a 60 bizonyos osztói többféleképpen is előállnak a 6, illetve a 10 prímtényezőinek kombinációjaként, ezáltal többször is beszámításra kerülnek az összegzéskor.

Például a 2, ami a 60 egyik osztója, egyúttal a 6-nak és a 10-nek is osztója, így mindkettő osztóinak összegében szerepel, de nyilvánvaló, hogy a 60 osztóösszegében csak egyszer kellene benne lennie. Ebből a megfigyelésből azonnal adódik, hogy a gyenge multiplikativitáshoz szükséges, hogy a szorzatban szereplő tényezők páronként relatív prímek legyenek, a korábbiak alapján pedig elégséges is. Másfelől a fenti példa azonnal kizárja, hogy az osztók összege (nem gyengén is) multiplikatív lehessen.

Az osztók hatványainak összege

Végezetül említsünk meg egy, a fentivel erősen rokon számelméleti függvénycsaládot, az osztók tetszőleges pozitív egész kitevőjű hatványainak összegét megadó függvényeket, összefoglalóan a s_k(n)-t is. Ez tulajdonképpen a s(n) osztóösszeg függvény kiterjesztése, általánosítása, ebből kifolyólag a kiszámítási módja is nagyon hasonló: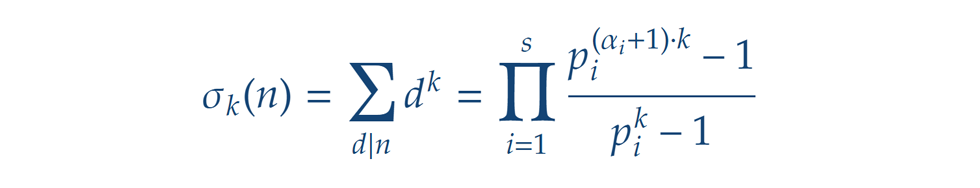A képlet levezetése lényegében ugyanaz, mint az osztók összege esetén annyi különbséggel, hogy az itt főszerepet játszó mértani sorozatok kvóciensei nem egyszerűen a felbontásban szereplő prím alapok, hanem azok k-adik hatványai.

Például, a 72 esetében az osztók harmadik hatványainak összege a következőképpen alakul.Miután elvégeztük a zárójelek felbontását, ugyanúgy soronként kiemelhetjük a közös tényezőket:Ismét kiemelve a zárójelet is: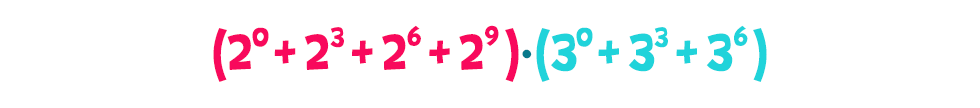A két zárójel ezúttal is egy-egy mértani sorozat első néhány tagjának összege, de az osztók összegével szemben most a kvóciensek a 2³ és a 3³, azaz eredményül a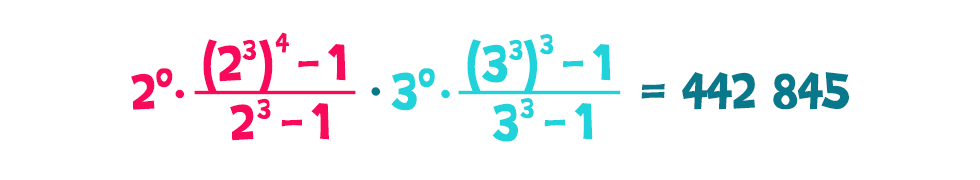adódik.

Forrás:

Megyesi László: Bevezetés a számelméletbe (Polygon Jegyzettár 1997)