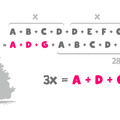
Lássuk a „Szorzótábla” feladvány megoldásának részleteit.

Mindenekelőtt, az első sor és a végeredmény alapján megállapíthatjuk, hogy lényegében egy négyjegyű számot emelünk négyzetre, és kapunk eredményül egy olyan nyolcjegyű számot, melynek utolsó négy számjegye épp az eredeti számot alkotja. A további hivatkozások megkönnyítése érdekében a négyjegyű szám legyen n = ABCD.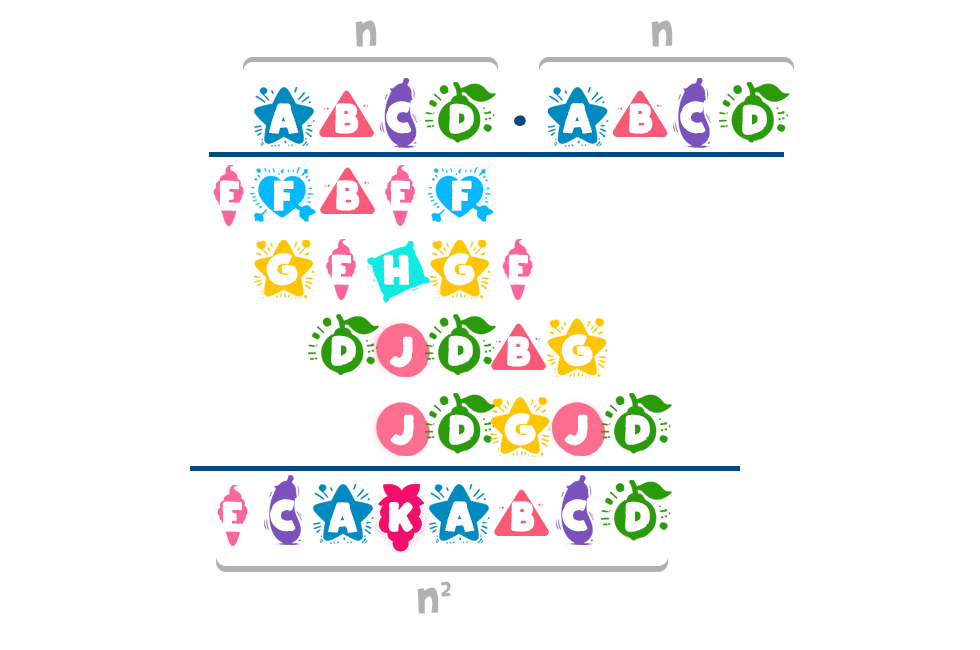Az első megfigyelésünk lehet az, hogy mivel a 3162 négyzete még 7-jegyű szám, de a 3163-é már 8-jegyű, n első számjegye, azaz az A nem lehet 3-nál kisebb. (A 0 mint kezdő számjegy egyébként sem megengedett, mert akkor nem négyjegyű a szám, de így az 1 és a 2 is kizárható.)

A következő észrevételünk, hogy egy tetszőleges egész szám négyzetre emelésekor az eredmény utolsó számjegyét az eredeti szám utolsó számjegye határozza meg. Könnyen igazolható, hogy a 0-ra, 1-re, 5-re vagy 6-ra végződő számok négyzetei lesznek az eredetivel megegyező végződésűek (pl. 21·21=441 vagy 156·156=24 336), a többié nem. Ezek alapján D csak a 0, 1, 5, 6 jegyek valamelyike lehet, e kör azonban tovább szűkíthető.

Bármely nyolcjegyű szám felírható valahányszor (pl. k-szor) 10 000 és egy 10 000-nél kisebb szám összegeként. Például a 12 345 678 = 12 340 000 + 5 678 = 1 234·10 000 + 5 678. Nincs ez másképp a végeredményként kapott nyolcjegyű számunkkal (n²-tel) sem, azaz: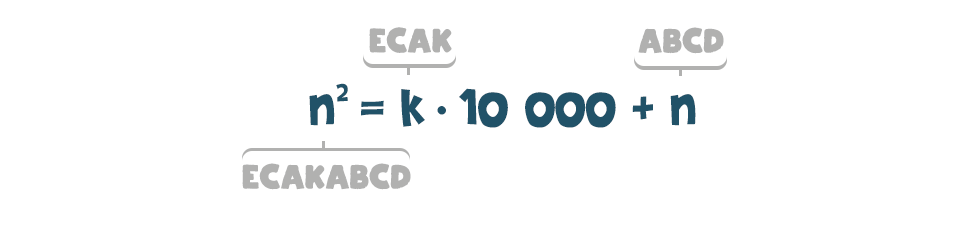valamilyen pozitív egész k-ra. Ezt kicsit átalakítva: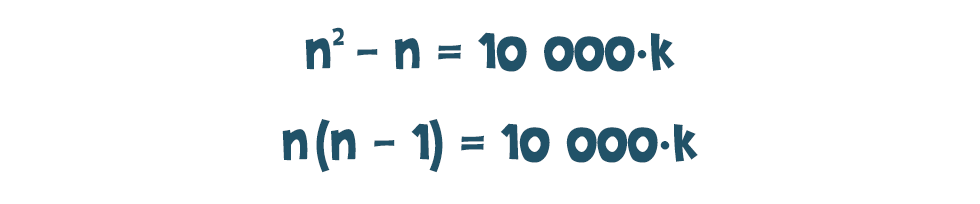ami így tulajdonképpen azt jelenti, hogy az n·(n-1) osztható 10 000-rel, azaz 10⁴-nel.

Mivel n-1 és n egymást követő egész számok, az egyikük biztosan páros (azaz 2-vel osztható), a másikuk pedig páratlan. A 10⁴ prímfelbontása 2⁴·5⁴, tehát, ha n·(n-1) osztható 2⁴·5⁴-nel, akkor az csak úgy lehet, ha n és n-1 közül a páros az, amelyik osztható a teljes 2⁴-nel, vagyis 16-tal, mivel a páratlan szám nem lehet osztható 2-vel. A páratlan viszont mindenképpen osztható lesz 5-tel, hiszen már csak olyan osztók jöhetnek szóba, amik az 5 hatványai, így ez a szám 5-re is kell, hogy végződjön.

Mindezek alapján két eset lehetséges. Az egyik, ha n-1 osztható 16-tal, ekkor viszont rögtön kapjuk, hogy n 5-tel osztható páratlan szám, így utolsó számjegye biztosan az 5. A másik lehetőség, hogy n a 16-tal osztható szám, ami azt jelentené, hogy utolsó számjegye mindenképp páros. D fent említett lehetséges értékei közül csak a 0 és a 6 ilyenek. Viszont ez esetben n-1-nek 5-re kell végződnie, így a D=0 eset ki is zárható. A két esetet összegezve, D=5 vagy D=6.

Ha D=5 lenne, akkor mivel az A·D szorzat F-re végződik (ld. ábra) F csak 0 vagy szintén 5 lehet. Mivel a különböző karakterek különböző számjegyeket jelentenek, az 5 kizárható, így szükségképpen F=0. Hasonlóan a B·D utolsó számjegye E, de D=5-re E is 0 vagy 5, viszont már mindkét számjegyet kiosztottuk D-nek és F-nek, így E=D vagy E=F állna fent, ami ellentmond a feltételeknek.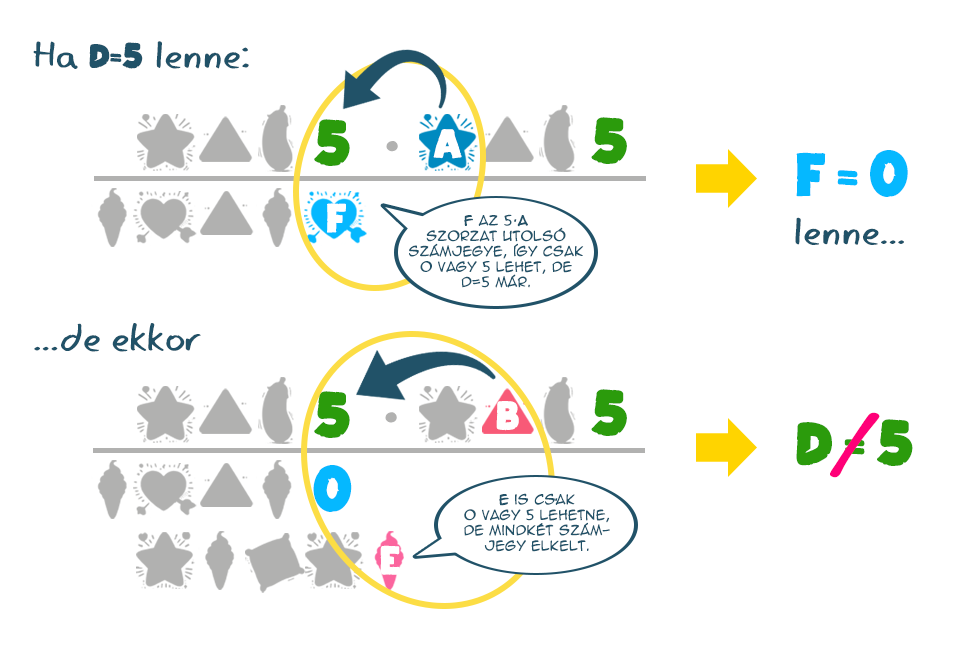Következésképpen D nem lehet 5, azaz egyetlen lehetőség marad, ha D=6.

Ha D=6, akkor n nem osztható 5-tel, tehát n-1 kell, hogy osztható legyen vele és ezáltal 5⁴-nel, azaz 625-tel is. Más szóval akkor, n-1 = 625·k alakú, de tudjuk azt is, hogy n-1 páratlan, így k is az. Mivel az A legalább 3, illetve 16·625 már ötjegyű lenne, a k lehetséges értékei 7, 9, 11, 13, 15. Végignézve a 625 ennyiszer vett többszöröseit, a tízesek helyén mindig a 2 vagy a 7 jelenik meg. (Általánosságban is igazolható, hogy a 625 páratlan számú többszöröseiben a tízesek helyén 2 vagy 7 áll.)

Mivel n 6-ra végződik, az n-1-re lépéskor nem történik tízes átváltás, tehát az iménti tulajdonság magára n-re is igaz lesz, más szóval C=2 vagy C=7. Igen, ám, de ha C=2 lenne, akkor n-nek 26-ra kellene végződnie, egy ilyen szám négyzetének viszont mindig 76-ra, ami ellentmondás, így C=7.

Innen már felgyorsulnak az események. A C·D szorzat eredményének utolsó számjegye a negyedik sor végén látszik. Mivel C·D=42, G=2.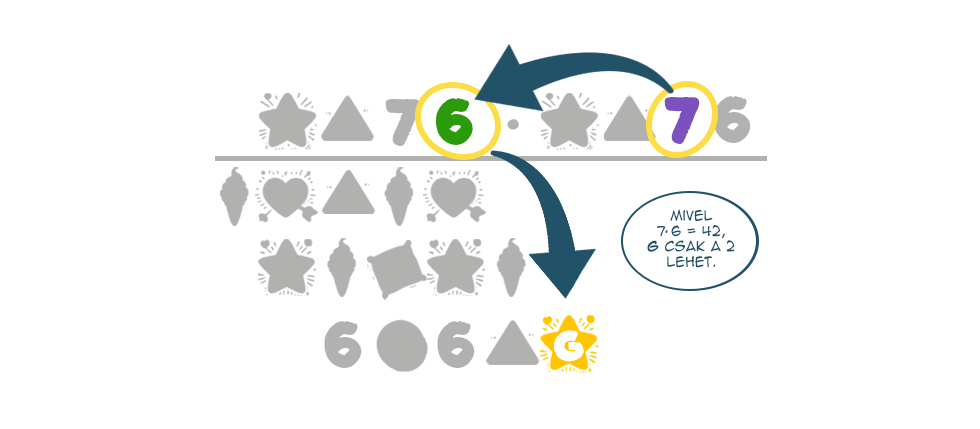Hasonlóan, a negyedik, az ötödik és az eredménysor alapján J=5.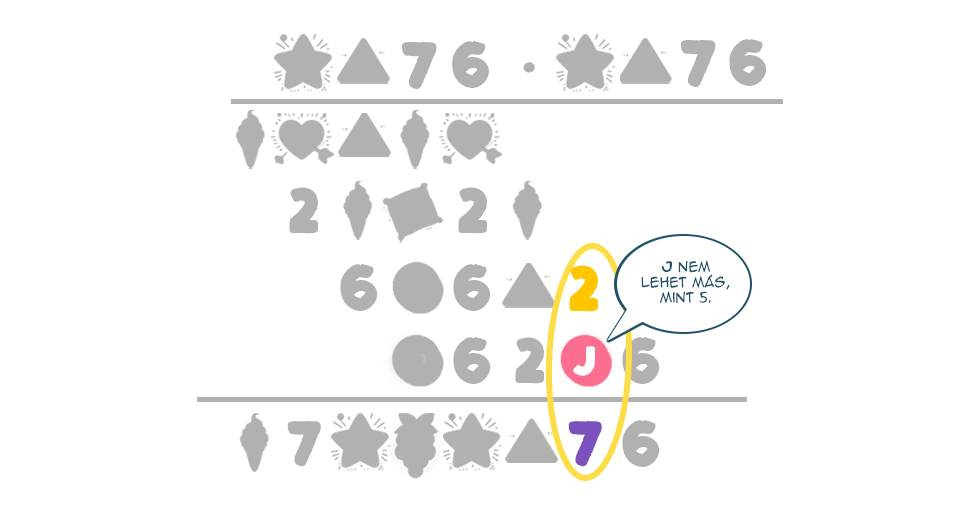Folytatva a visszafejtést E=8 lesz: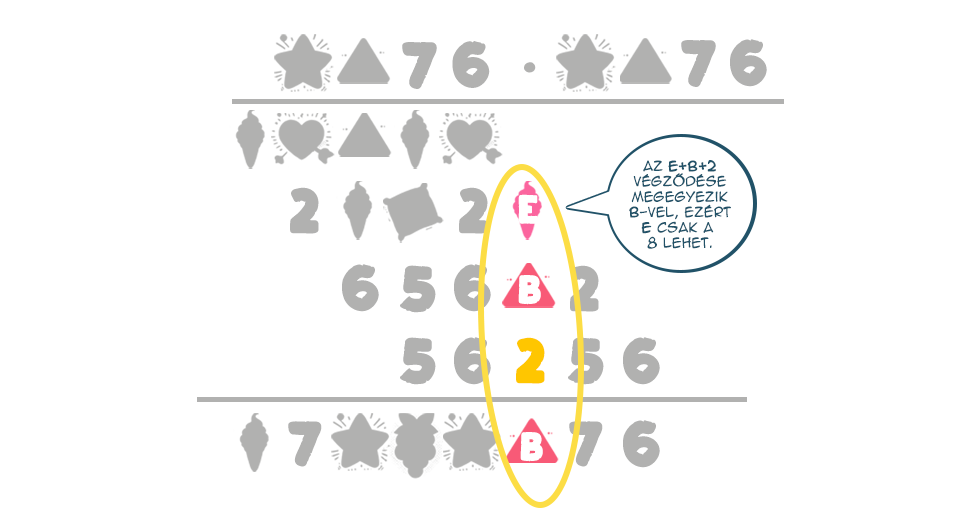

Ez alapján pedig, mivel B·D utolsó jegye 8, B=3 lesz: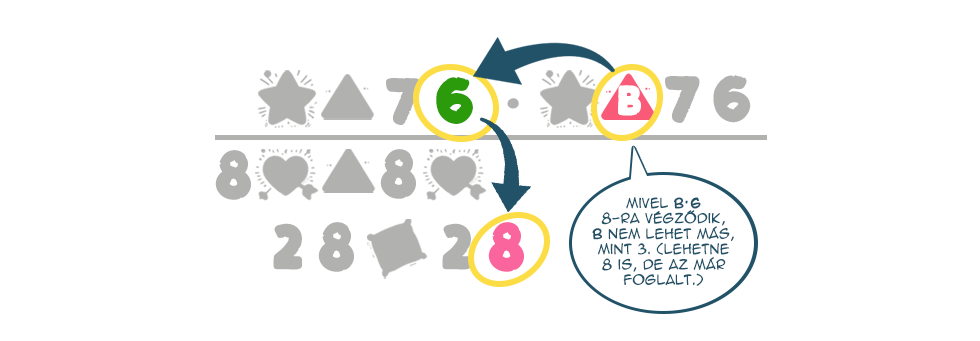

Térjünk vissza egy kicsit az első két sorra. Ezek alapján F az A·6 szorzat végződése, így mindenképpen páros számjegy. Ilyenekből viszont már csak a 4-es maradt, tehát F=4.

Ez viszont egyúttal azt is jelenti, hogy A csak 4 vagy 9 lehet, de a 4-est épp az imént osztottuk ki, vagyis A=9.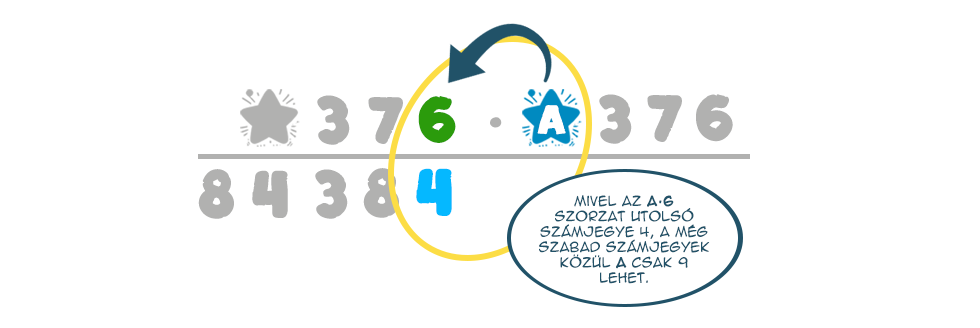

Ezzel meg is kaptuk, hogy n=9376. Most, hogy megvan n értéke, minden még fennálló hiányosság is kitölthető, azaz H=9 lesz: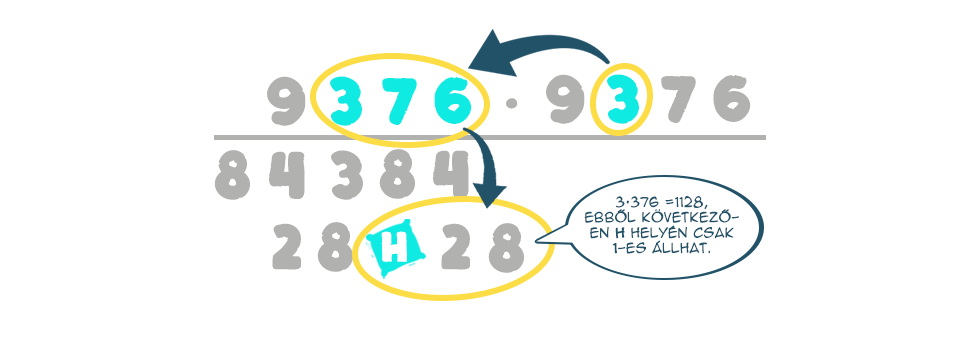K pedig végül 0: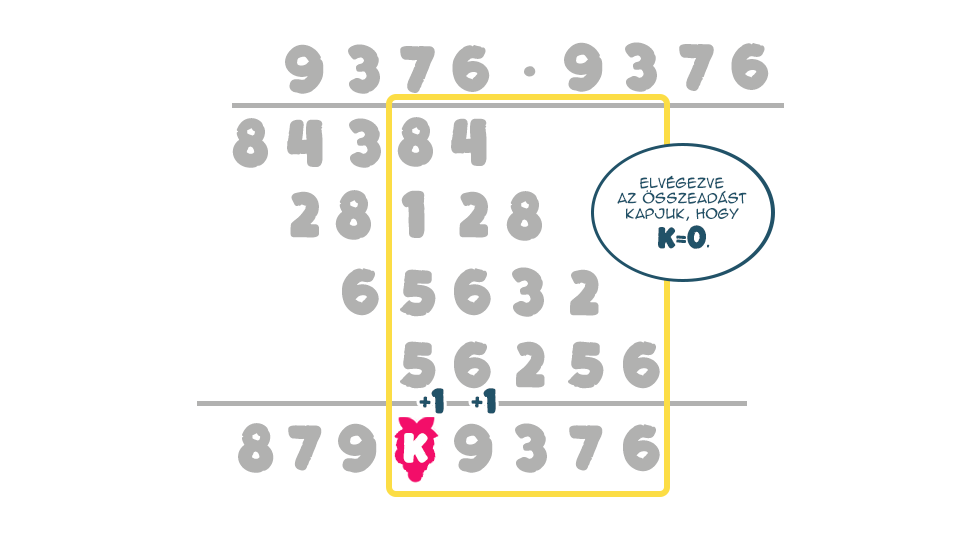

A megfejtés tehát:

▪