Kalózok és holdacska
A matematika egyik legendás és egyben elátkozott problémája a kör négyszögesítése, azaz egy olyan négyzet megszerkesztése, ami egy adott kör területével megegyező területű. A remény a feladvány megoldására legkésőbb 1882-ig, a p transzcendens voltának bizonyításáig (ami Ferdinand von Lindemann nevéhez köthető) élhetett, ami azonban véget vetett az álmoknak.
A probléma felvetődése időben jóval korábbra tehető, már az ókori görög matematikusokat is foglalkoztatta a kérdés. Közéjük tartozott khioszi Hippokratész, Kr. e. 5. századi kereskedő is (aki nem azonos az orvos Hippokratésszal). A fáma szerint egyik kereskedelmi útján kalóztámadás érte, aminek következtében minden vagyonát elveszítette. Igazságszolgáltatás reményében Athénba utazott, viszont a jogi procedúrák akkoriban sem zajlottak villámgyorsan, így volt ideje huzamosabb időt eltölteni a városállamban. Eközben számos filozófussal volt szerencséje társalogni, ami komoly hatással volt geometriai ismereteire is. Alighanem ennek köszönhető, hogy a kör négyszögesítésének problémájáról egyáltalán tudomást szerzett.
Egyetlen ismert műve az Elemek címet viselte (nem Eukleidész azonos című művéről van szó), és különlegessége, hogy korától némileg szokatlan módon, nagy hangsúlyt fektetett a precíz bizonyításokra. Maga a könyv elveszett, de rodoszi Eudémosz a Geometria története című írásában megtalálhatóak voltak bizonyos részletei. Sajnos ez a mű sem maradt fenn, viszont ebből ismerhetjük (nem teljesen ebben a formában) Hippokratész alábbi tételét.
Hogy jön ez a kör négyszögesítéséhez? A tétel legnagyobb erénye, hogy egy csupán körívek által határolt síkidom területét sikerült „átvinnie” egy egyenes szakaszok által határolt síkidomba, esetünkben egy háromszögbe. A tény a „négyszögesítők” számára rendkívül reménykeltő volt.
Bizonyítás
Modern szemmel a bizonyítás nem nehéz, nagyjából a nyolcadikos matematikai anyag ismerete is elég hozzá. A Thalész-kör sugara a derékszögű háromszög átfogójának fele, így a félkör területe könnyen számolható. Ha ezt egyesítjük a háromszöggel, majd összterületükből elvesszük a negyedkör területét, a megmaradó síkidom területe épp a háromszög területével fog megegyezni.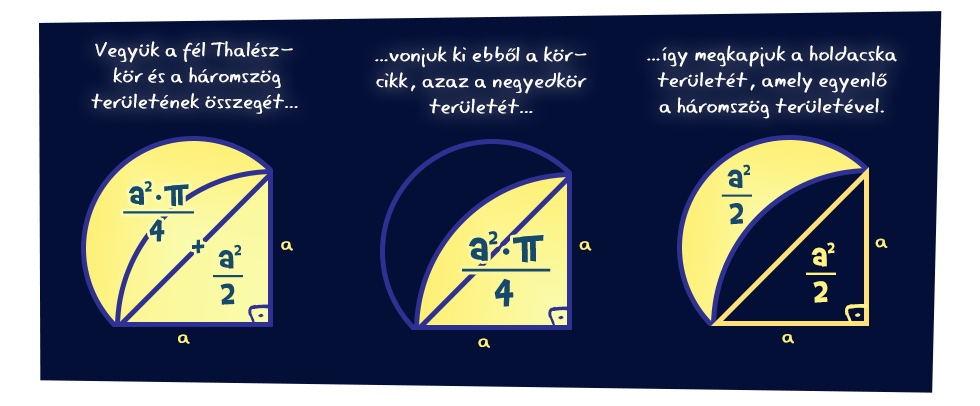
Al-Hajszam holdacskái
Az arab matematikus, Ibn al-Hajszam nevéhez fűződik a tétel egy másik, általánosabb formája. Eszerint, ha egy tetszőleges derékszögű háromszög befogóira írunk egy-egy olyan félkört, melyek átmérői maguk a befogók, majd ezek területeiből kivonjuk azokat a részeket, amiket a háromszög Thalész-köre is tartalmaz, akkor a keletkező holdacska alakú síkidomok összterülete egyenlő lesz a háromszög területével.
Bizonyítás
E tétel igazolása sem vészes. A befogókra szerkesztett félkörök területei kiszámíthatók a befogók (mint átmérők) hosszai segítségével. Adjuk hozzá ezeket a háromszög területéhez, majd vonjuk ki a kapott eredményből a Thalész-kör területének felét. A Pitagorasz-tételt is felhasználva így a holdacskák összterülete éppen a derékszögű háromszög területével lesz egyenlő.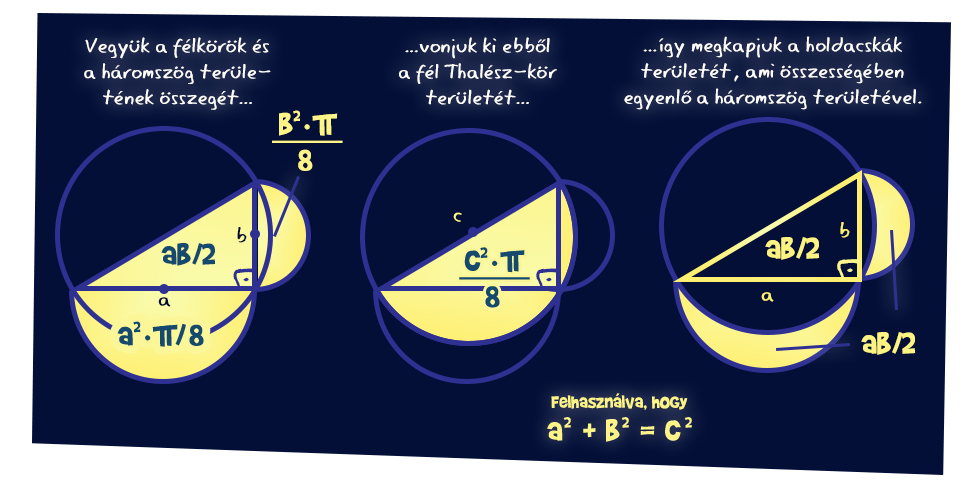
Húrnégyszögek
Ha két egyforma átfogójú derékszögű háromszöget összeillesztünk az átfogóiknál, akkor egy olyan négyszöget kapunk, amiben két szemközti szög derékszög, ezáltal a másik két szög összege is 180°. Ez tehát egy speciális húrnégyszög, amire a fentiek alapján könnyen látható, hogy teljesül az alábbi tulajdonság. (Emlékeztetőül, a húrnégyszögek olyan négyszögek, melyeknek van körülírt körük.)
A négyszög oldalaira mint átmérőkre félköröket írva, azokból a húrnégyszög köréírt köre által tartalmazott területeket elhagyva a megmaradó négy holdacska összterülete egyenlő lesz a négyszög területével.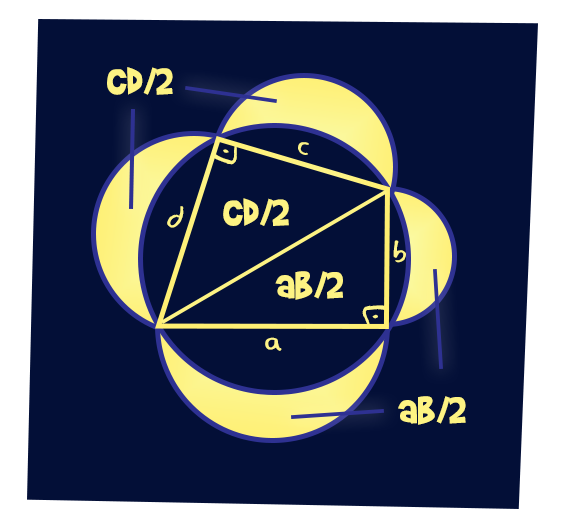
Sajnos ennél tovább viszont nem mehetünk. Nem derékszögű húrnégyszögekre általában nem jelenthető ki hasonló tulajdonság, jó példa erre egy 60°-os vagy egy 45°-os húrtrapéz esete.
Források:
https://dynamicmathematicslearning.com/hippocrates.html
https://en.wikipedia.org/wiki/Lune_of_Hippocrates
https://hu.wikipedia.org/wiki/Khioszi_Hippokrat%C3%A9sz
Ajánlott bejegyzések:
A bejegyzés trackback címe:
Kommentek:
A hozzászólások a vonatkozó jogszabályok értelmében felhasználói tartalomnak minősülnek, értük a szolgáltatás technikai üzemeltetője semmilyen felelősséget nem vállal, azokat nem ellenőrzi. Kifogás esetén forduljon a blog szerkesztőjéhez. Részletek a Felhasználási feltételekben és az adatvédelmi tájékoztatóban.
