Középiskolásként még gyanúval vegyült kíváncsisággal nézegeti az ember a számológépén az e^x és ln gombokat, amik gyakran épp ugyanannak a gombnak két külön funkcióját takarják. Később aztán ki az emelt matek csoportban, ki az egyetemen megismerkedik az e-vel, azaz az „Euler-féle” számmal, és a természetes alapú logaritmussal, az ln-nel is. Fény derül a kettő közti inverz kapcsolatra, ezáltal arra is, hogy az ln épp az e alapú logaritmust takarja. Felvetődik viszont a kérdés, hogy ha az ln az e alapú logaritmus, akkor miért ln-ként rövidítjük, miért nem le-ként vagy valami egyéb, az e-re utaló módon. A válasz a felfedezéseik ideiben rejlik.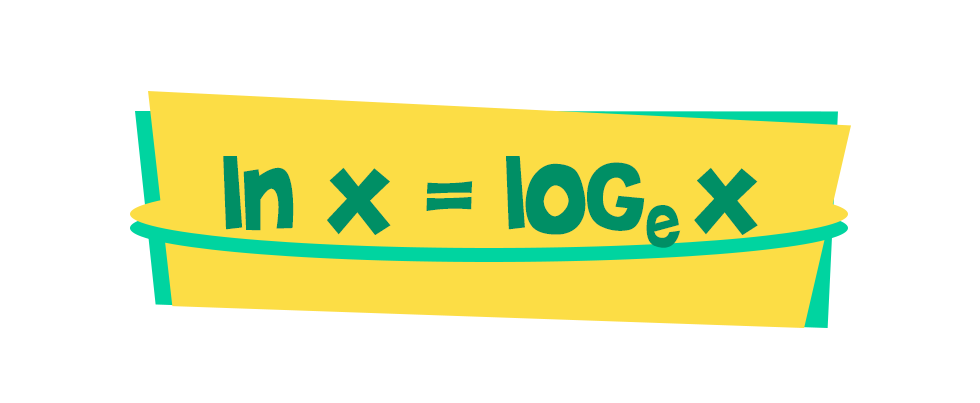

Praktikum

A logaritmusok felfedezése, használatuk bevezetése modern szemmel meglepően koránra tehető. Noha egyes források szerint a svájci matematikus, Joost Bürgi már korábban is kerülgette a témát, mivel eredményeit meglehetősen ráérősen publikálta, a skót teológus és matematikusé, John Napieré lett a dicsőség a logaritmus első megjelenését illetően. Napier 1614-ben megjelent műve, a Mirifici Logarithmorum Canonis Descriptio központi témája lényegében logaritmustáblák felépítése, logikája és használata. Későbbi műve, a Mirifici logarithmorum canonis constructio, mely halála után jelent meg, tovább segítette a módszer elterjedését.

A felfedezés magasztos, az alapvető motiváció viszont kényelmi jellegű volt. A korabeli, a kamatokkal előszeretettel számoló bankárok szerették volna, ha egyszerűbben és ezáltal persze gyorsabban lehetne elvégezni a kamatos kamatnál fellépő számításokat. Bürgi például a kamatos kamatot meghatározó mértani sorozatot egy számtani sorozat tagjaival „váltotta ki”. Matematikailag a probléma mélyén egy aritmetikai feladvány található. Miként lehet a szorzás és osztás műveleteket összeadásokra és kivonásokra egyszerűsíteni?

Napier logaritmusa

Napier egy másik alapproblémán keresztül jutott el ugyanide. Egy olyan mozgás közelítő leírásával foglalkozott, mely esetén egy adott pillanatban a sebesség mértéke éppen a hátralévő út hosszával egyezik meg. Levezetéseinek eredménye lett a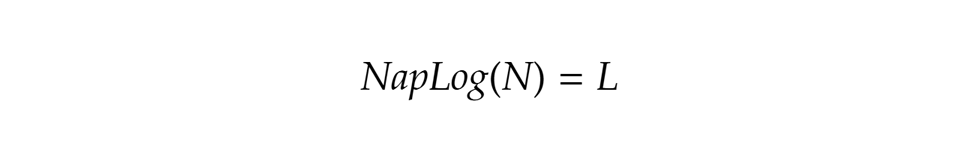szám, amit mai megfogalmazásban az N szám L alapú logaritmusának nevezhetnénk. A név a görög logosz (arány) és arithmosz (szám) összetételéből ered. A fenti kifejezés azt jelentette, hogy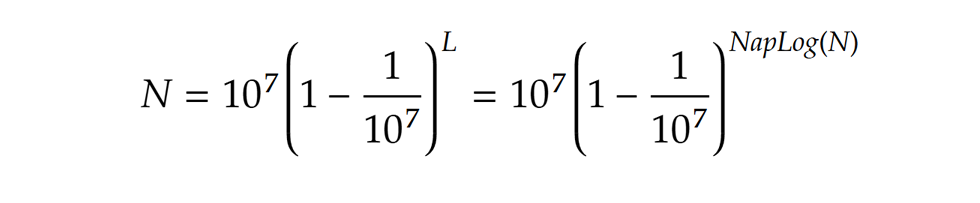Az 1/10⁷ magyarázata prózai, Napier ekkora hosszúságú intervallumokra osztotta fel az időt a mozgás vizsgálatakor. A konstrukció, noha némileg eltér a modern logaritmusétól, valóban eléri a kívánt célt. A NapLog segítségével a szorzás és az osztás „kiváltható” összeadással és kivonással.

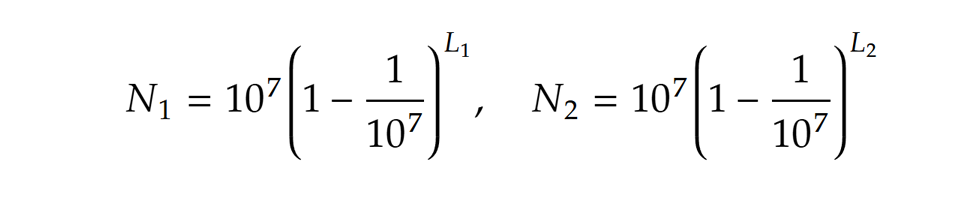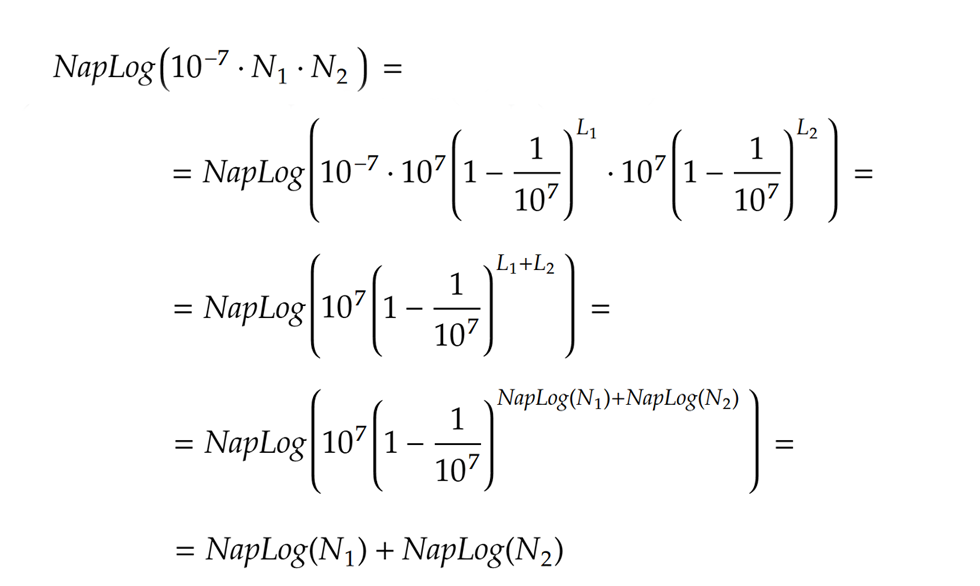Például, haakkorilletve hasonlóan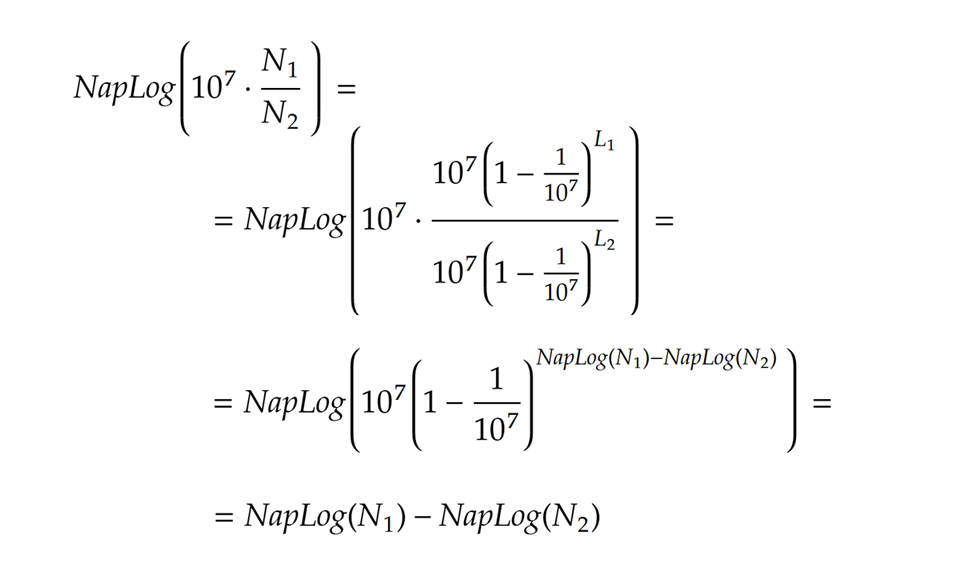Messze nem Bürgi és Napier voltak azonban az egyetlenek, akik munkáiban megjelent a logaritmus.

A hiperbola

A modern matematikában jól ismert tény, hogy az ln(x) függvény az 1/x egy úgynevezett primitív függvénye, azaz az ln(x) deriváltja az 1/x. Mivel a törtfüggvény grafikonja egy hiperbola, így az integrál alapkoncepciója alapján: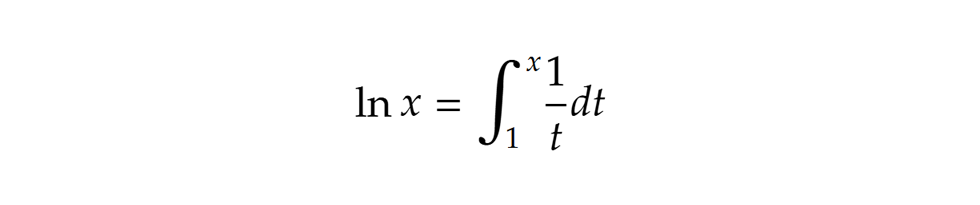Más szóval, az 1/x függvény grafikonja alatti terület az [1;x] intervallumon tökéletesen megadja az ln(x) értékét minden 1-nél nem kisebb x-re. A források szerint mindez (persze nem ebben a formában) megtalálható a jezsuita matematikus, Alphonse Antonio de Sarasa 1649-es, Solutio problematis a R.P. Marino Mersenne Minimo propositi című írásában, illetve mesterének, Gregoire de Saint-Vincentnek a Opus Geometricum című művében is. Már Saint-Vincentet is foglalkoztatta a kérdés, hogy mit válasszunk a grafikon és az x-tengely közötti síkidom jobb oldali határának, hogy a síkidom területe éppen 1 legyen.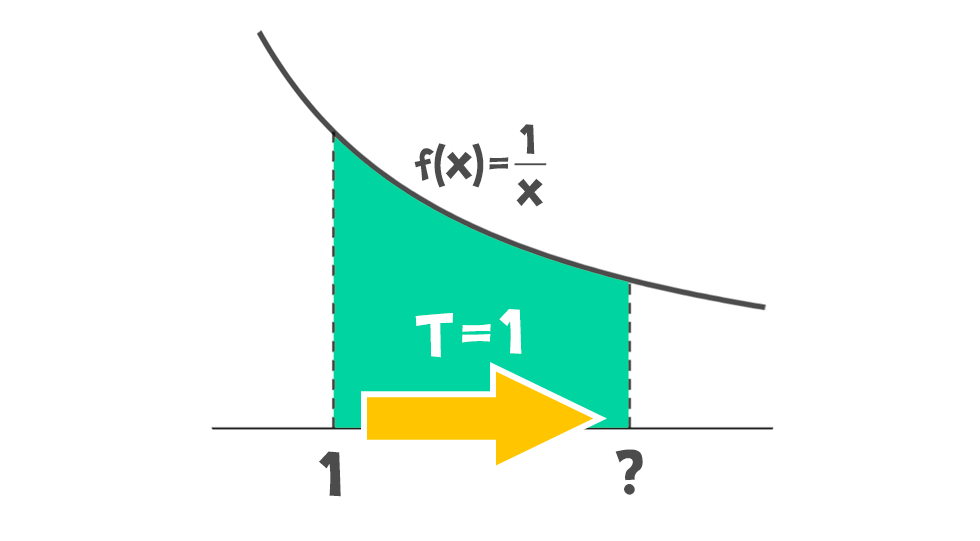Persze ma már tudjuk, hogy ezt a határt az e szám adja, azaz burkoltan az ln és az e közötti kapcsolat már itt felvillant. A bökkenő, hogy ekkortájt Leonhard Euler még meg sem született, az e számról pedig még senki nem is hallott.

A láthatatlan szám

Mai szemmel világos, hogy az e már ott volt Napier, Saint-Vincent és Sarasa munkáinak hátterében, de akkoriban senki nem fedezte még fel, legalábbis nem tett róla említést. Ismereteink szerint bizonyítottan a holland tudós, Christiaan Huygens volt az első, aki megértette a hiperbola alatti terület és a logaritmus kapcsolatát. Ő is vizsgálta a Saint-Vincent által már felvetett kérdést (hogy az xy=1 egyenletű hiperbola alatti terület mikor is lesz pontosan 1), de az e számig ő sem jutott el. Huygens később ugyan az y=ka^x egyenletű görbe vizsgálatakor még közelebb került az e felfedezéséhez, azonban a számításai során csak az e 10-es alapú logaritmusáig jutott el, ami egyrészt nem számított új eredménynek, másrészt ez Huygensnél is megmaradt egyszerű konstans szerepkörben, nem pedig bármiféle szám logaritmusként.

Valamivel később újabb esély nyílt az e megtalálására, Nicolaus Mercator 1668-as, Logarithmotechnia című művében megtalálható egy sorfejtés, ami épp az ln(1+x)-et adja, az e viszont továbbra is rejtve maradt. A mű egyébként azért is fontos, mert a források szerint ez volt az első alkalom, hogy a természetes alapú logaritmus kifejezés leírásra került.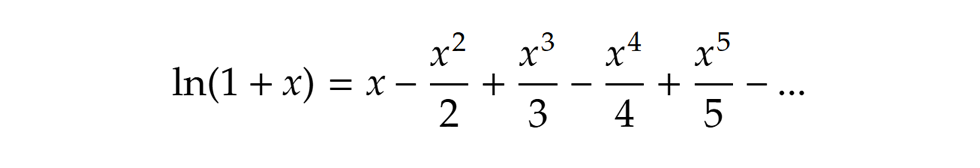

Bernoulli és a kamatos kamat

A sok elszalasztott lehetőség után ott sikerült fülön csípni az e-t, ahol az egész történet elkezdődött. A neves bázeli matematikuscsalád sarja, Jacob Bernoulli a folytonos kamatozás vizsgálata során botlott bele a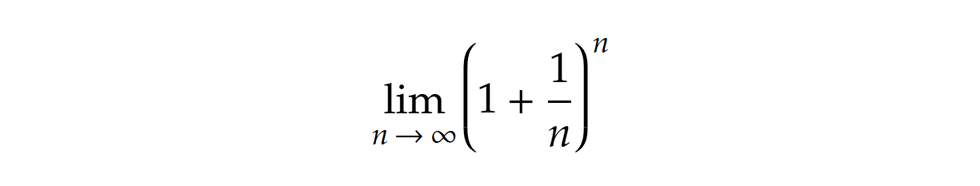határérték keresésének kérdésébe. Vizsgálódásai során Bernoullinak a binomiális tétel segítségével sikerült igazolnia, hogy a sorozat határértéke valahol a 2 és a 3 között van. Ma már jól tudjuk, hogy a határérték pontosan az e szám, ami kerekítve 2,71828… (Sőt, ez maga az e definíciója is.) Persze az említett becslés egy elég durva közelítés, de immáron mindkét kirakósdarab az asztalon hevert.

Mindezek ellenére minden bizonnyal Bernoullinak sem tűnt fel az e logaritmussal való kapcsolata. James Gregory, skót matematikus 1684-ben viszont már egész biztosan felismerte, hogy a logaritmus és az exponenciális függvény egymás inverzei, viszont kérdéses, hogy ő volt-e az első.

Ismereteink szerint tényleges valójában 1690-ben bukkant fel először az e Leibniz egy Huygensnek írt levelében, ám ekkor még b néven. Nem sokkal később, 1697-ben Johann Bernoulli (Jacob öccse) megjelentette Principia calculi exponentialium seu percurrentium című művét, melyben fellelhetőek az exponenciális függvény tanulmányozásának első lépései, ami újabb fontos állomást jelentett az e korai történetében. Tanulmányozásának dandárja azonban nem ehhez a műhöz, sokkal inkább az e „hamis” névadójához köthető.

Euler száma

Jelen tudásunk szerint az e jelölést Leonhard Euler vezette be, de ismerve a személyiségéről szóló írásokat, nem valószínű, hogy a saját nevének kezdőbetűje lett volna ennek oka. Egyes források szerint az e inkább az exponenciális vagy az exponens (kitevő) szóból eredhet, más vélekedések alapján viszont egyszerűen csak annyiról lehetett szó, hogy Euler nem akarta a már sok helyen használatban lévő a betűt használni ebben a speciális esetben, de mindenképpen magánhangzót szeretett volna, így került sor ez e-re. Ami viszont bizonyos, hogy az e jelölés Euler 1731-es, Goldbachnak írt levelében már szerepelt.

Valamivel később, 1748-ban az Introductio in Analysin infinitorum című könyvében aztán Euler kifejtette az e tanulmányozása során kapott eredményeit. Számos további érdekes tulajdonság mellett bebizonyította például, hogy a Jacob Bernoulli által tanulmányozott határérték valóban az e, illetve, hogy előáll az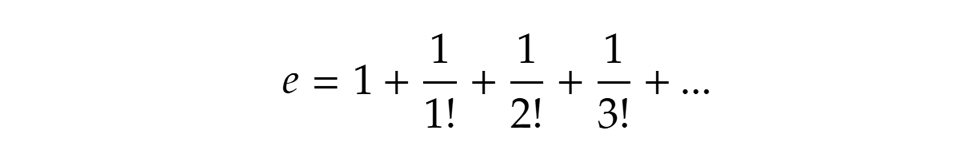alakban, de kiszámította (valószínűleg a sorfejtés alapján, de erre nincs közvetlen bizonyíték) az e első 18 tizedesjegyét is: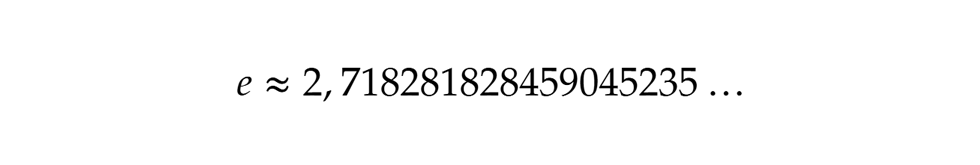

Természetesség

Végül lássuk a természetes jelző létjogosultságát. Az exponenciális függvények körében lényegében egyetlen olyan típusú van, amire igaz, hogy egy adott pontjában a pillanatnyi meredeksége megegyezik a függvény ottani értékével, ez pedig nem más, mint az e^x. Modern matematikai nyelven, az e^x deriváltja saját maga. Ha a meredekségre úgy tekintünk, hogy az a pillanatnyi változást jelenti abban a folyamatban, amit az adott függvény leír, akkor ez más szóval azt mondja, hogy az adott pillanatbéli változás éppen az adott állapotot tükrözi. Kicsit kiterjesztve, a folyamat pillanatnyi változása arányos a pillanatnyi állapottal.

Az imént leírtak megfordítva remekül illeszkednek Napier problémájára. A sebesség egy bizonyos idő (dt) alatt a megtett út változása (ds). Ha ez egyben a megtett út hossza (s) is - ami lényegében a hátralévő úttal kölcsönösen egyértelmű viszonyban áll - akkor kissé pongyolán, kiegészítő konstans szorzókat mellőzve, az alábbi differenciálegyenlet írható fel: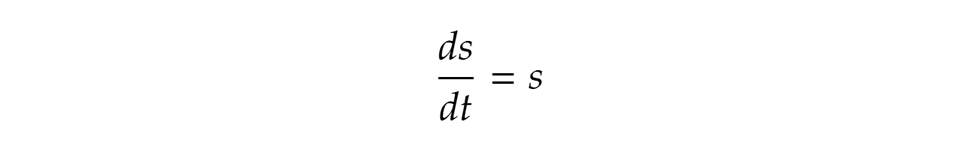Ennek megoldása a változók szétválasztása után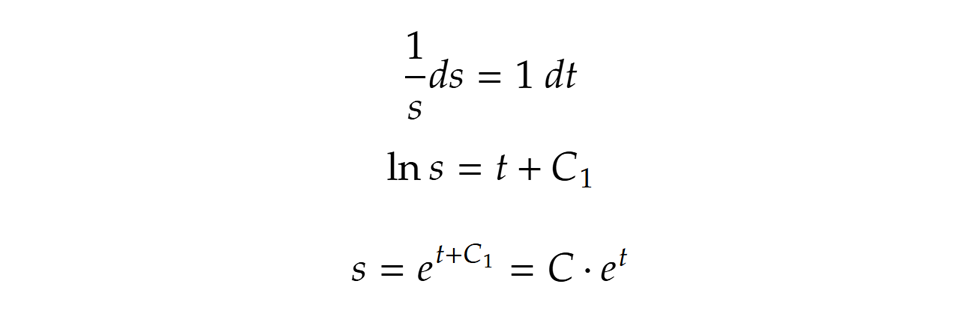valamilyen C konstanssal (persze s pozitív). Ha az időt akarjuk kifejezni, az a megtett út e alapú logaritmusával írható le. Ha az utat, az pedig egy e alapú, az időt a kitevőben tartalmazó hatvánnyal.

Hasonló egyenletek írhatók fel például a populációdinamikában, amikor is egy populációban a (nettó) szaporodás mértéke (azaz a változás) arányos az aktuális egyedszámmal (dx/dt = kx). Az idő itt is lényegében az egyedszám e alapú logaritmusával jellemezhető, az egyedszám pedig az e valamilyen időtől is függő hatványával. Kell-e ennél természetesebb példa vagy ok?

Végszó

Most már világos, hogy a természetes alapú logaritmus miért nem kaphatott az e-re utaló nevet. Egyes vélemények szerint az ln jelölésben az n akár Napier nevére is utalhatna, de ez nem túl valószínű magyarázat, hisz ilyen alapon az NL vagy nl sokkal érthetőbb volna. Az n betű minden bizonnyal valóban a természetes szóra utal, de szintén nem a legvalószínűbb, hogy az angol natural szó miatt. Sokkal esélyesebb a latin eredet, amit alátámaszt az a tény, hogy az osztrák matematikus, Anton Steinhauser 1875-ben már bizonyosan használta az ln. rövidítést a logarithmus naturalisra.

Források:

https://hsm.stackexchange.com/questions/42/which-came-first-the-natural-logarithm-or-the-base-of-the-natural-logarithm

https://mathworld.wolfram.com/NapierianLogarithm.html

https://hu.wikipedia.org/wiki/John_Napier_(matematikus)#%C3%8Dr%C3%A1sai

https://hu.wikipedia.org/wiki/Logaritmus

https://en.wikipedia.org/wiki/Alphonse_Antonio_de_Sarasa

https://mathshistory.st-andrews.ac.uk/HistTopics/e/

https://www.komal.hu/cikkek/kg/e/e.h.shtml

https://www.purplemath.com/modules/logs3.htm