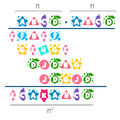
A Tojásgyűjtés feladatban egy gráffal találjuk szemben magunkat, melynek pontjai az ábrán lévő tojások, élei pedig az összekötő fehér útszakaszok. A feladat szerint olyan útvonalat kell keresnünk, ami végighalad a gráf pontjain úgy, hogy egyikbe sem tér vissza. Az ilyen utat a gráfelméletben Hamilton-útnak nevezzük.

Induljunk ki a gráf valamelyik pontjából, például A-ból, és fessük be mondjuk lilára. Ezt követően azokat a pontokat, amikbe az elsőként színezett pontból közvetlenül eljuthatunk, azaz C-t és D-t, színezzük be egy másik színnel, például sárgával. Folytassuk az eljárást úgy, hogy most a sárga pontok még nem színezett szomszédait színezzük be ismét lilára, ha ez lehetséges, azaz ezek az újonnan színezendő pontok nem szomszédai az első lila pontnak.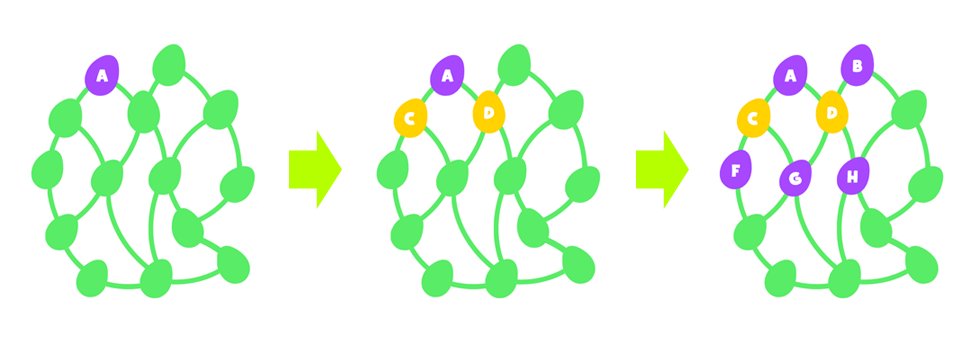Folytatva az algoritmust, arra jutunk, hogy a gráf minden pontját be tudjuk színezni e két szín valamelyikével. Az ilyen gráfot páros gráfnak hívjuk.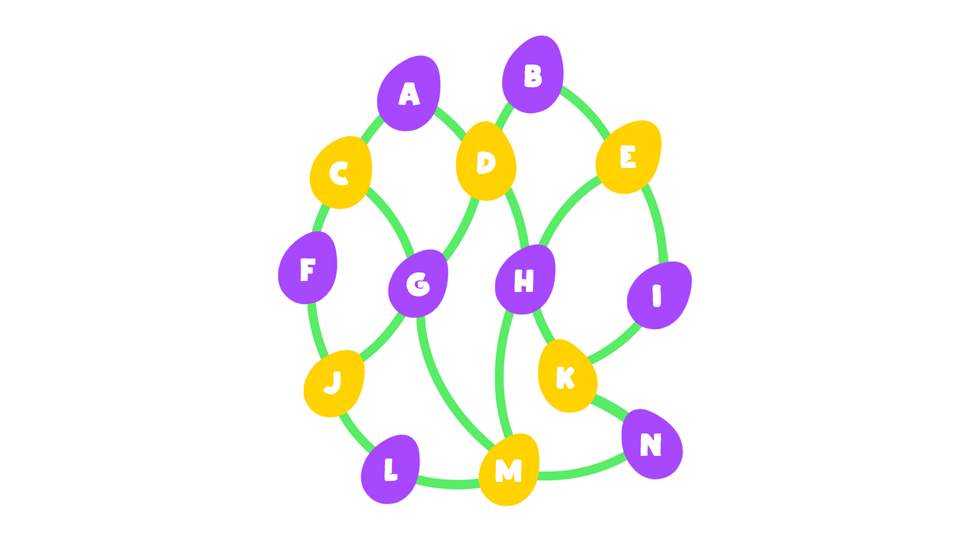A páros gráf lényegében azt jelenti, hogy a színek alapján a gráf pontjai két csoportba oszthatók úgy, hogy az azonos csoporton belüli pontok között nem fut él. Ebből következően, ha egy páros gráfban létezik Hamilton-út, azaz végig tudunk menni a kért módon, akkor a különböző színű pontok, jelen esetben tojások, váltakozva kell, hogy következzenek: egy lila után egy sárga, utána ismét egy lila stb. Ez viszont azt is jelenti, hogy a lila és sárga pontok számának vagy meg kell egyeznie, vagy esetleg az egyikből épp 1-gyel van több.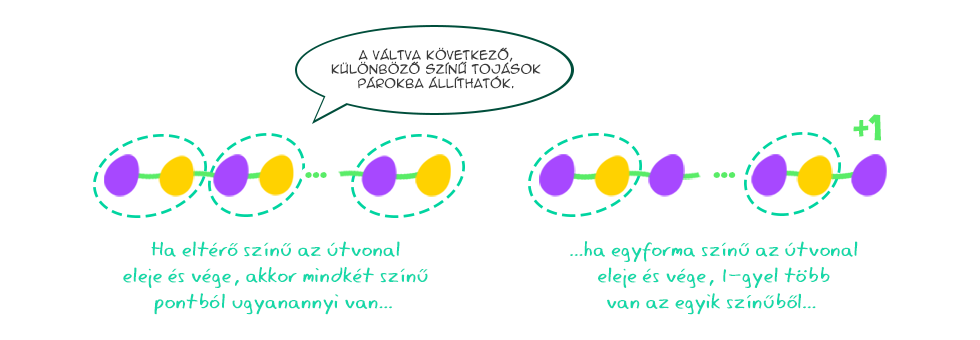A mi gráfunkban viszont 8 lila és 6 sárga pont van, azaz a feltétel nem teljesül, tehát a gráf pontjain nem lehet végigmenni a kívánt módon.

Egy kérdés maradt nyitott, vajon, ha másik ponttal kezdtük volna el a színezést, akkor nem lehetséges-e, hogy kijön 7-7 lila és sárga színű pont? A válasz nem ugyanis, ha például bármelyik jelenleg lila csúcsból kezdtük volna a színezést, és azt ismét lilára színezzük, akkor annak szomszédai ugyanúgy sárgák lennének, amiknek a szomszédai pedig ugyanúgy lilák, és így tovább. Ha egy jelenleg lila csúcsot sárgára színeznénk át, akkor pedig csak annyi történne, hogy az első színezéshez képest minden pont a másik színt kapná.