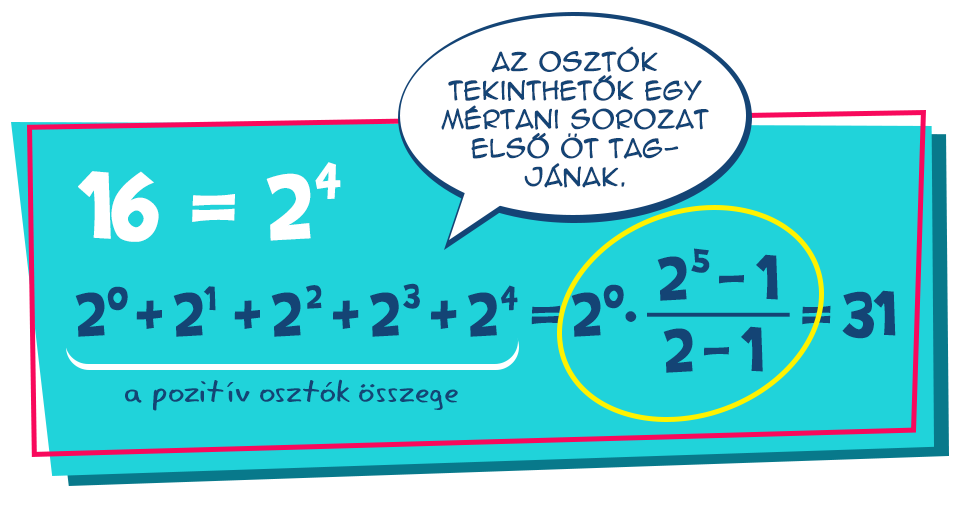
Hasonlóan ahhoz, ahogyan a természetes számok pozitív osztóinak számát meghatároztuk, megkaphatjuk ezen osztók összegét is az adott természetes szám prímtényezőinek ismeretében. Így egy újabb számelméleti függvényt kapunk, ami sok hasonlóságot mutat az osztók számát megadó függvénnyel.

A félreértések elkerülése végett, ezúttal is, amíg mást nem mondunk, osztók alatt csak a pozitív osztókat értjük majd, illetve szintén jegyezzük meg, hogy mivel ...

Egy pozitív egész szám osztóinak számát meghatározhatjuk azok konkrét felírása nélkül is a szám prímtényezős felbontása ismeretében. Ahhoz, hogy lássuk, ez egész pontosan hogyan is történik, vizsgáljuk meg először a legegyszerűbb eseteket. Mindenekelőtt, az 1-nek egyetlen pozitív osztója van, saját maga, a prímszámoknak pedig – a prím tulajdonság értelmében – két-két darab, az 1, és önmaguk.

A számok felépítését tekintve a következő szintet ...

Amikor az oszthatósági szabályokat tárgyaljuk, a 7-eshez érve gyakran elhangzik, hogy van rá szabály, de túl komplikált, ezért inkább nem is foglalkozunk vele, letudjuk a dolgot ennyivel. Ennek a bejegyzésnek a témája e „rejtély” feltárása lesz.

A közepébe vágva, egy szám akkor osztható 7-tel, ha számjegyeket hátulról hármasával csoportosítva majd váltakozó előjellel összeadva, a kapott eredmény 7-tel osztható. Például az 1 638 763 osztható ...

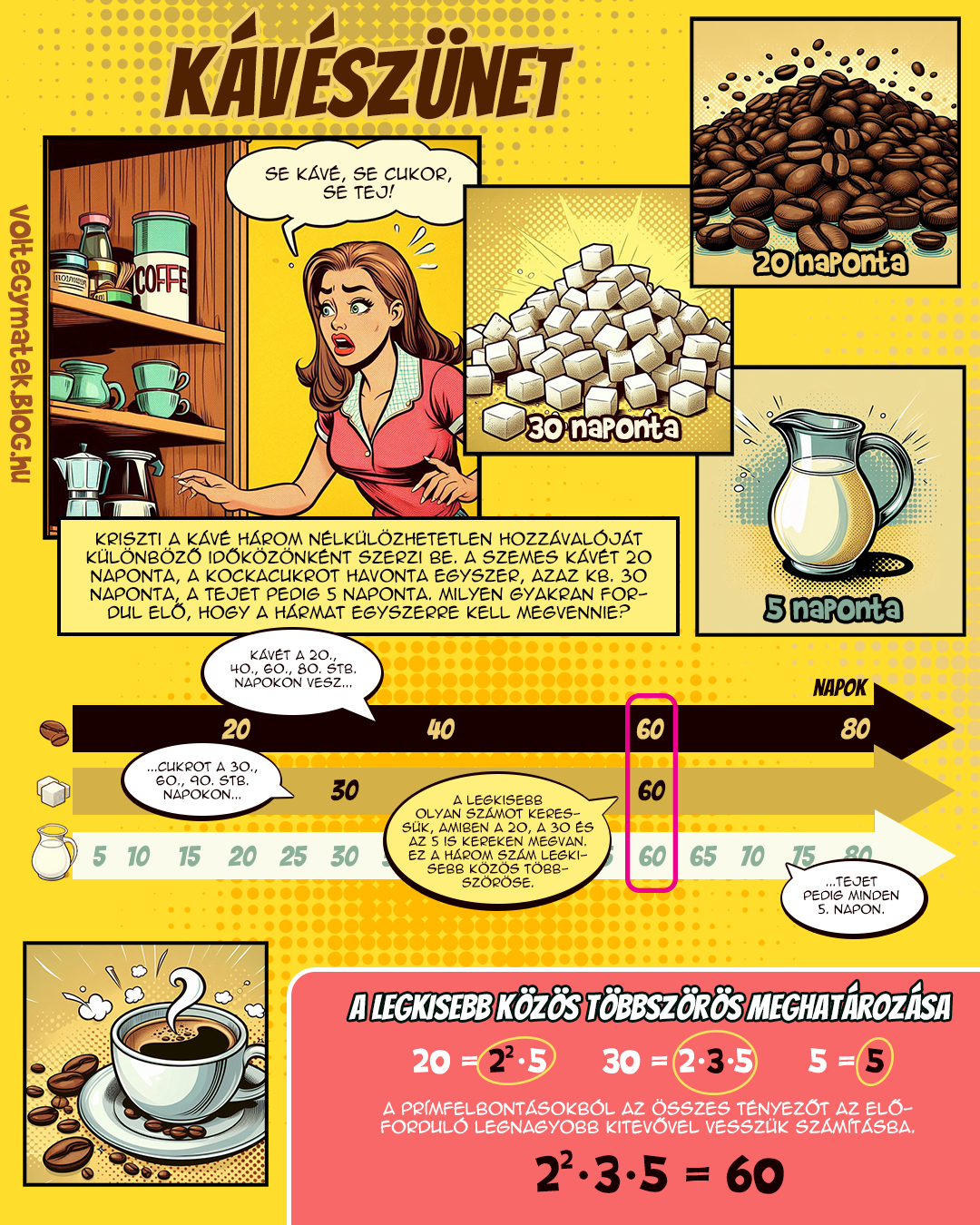
Két szám legnagyobb közös osztójának meghatározása a számok prímtényezős felbontásának birtokában könnyű feladat. Vannak azonban más módszerek is, közülük is a legismertebb talán az euklideszi algoritmus.

Euklidész lemmája

A módszer alapja, hogy bármely két pozitív a és b  egész szám esetén egyértelműen létezik olyan nemnegatív  q és r  egész (ahol fontos, hogy r kisebb b -nél) úgy, hogy: 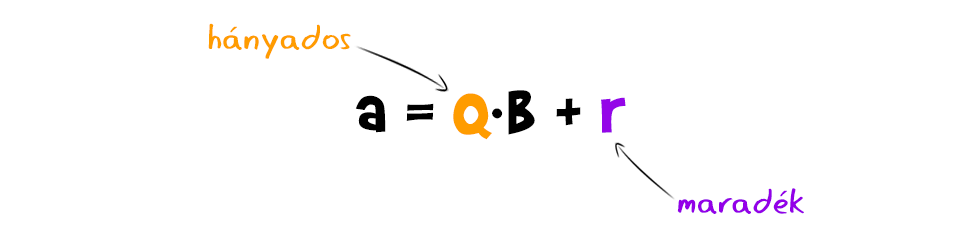azaz az egyik szám ( a ) előáll a másik ( b ) ...

Kezdésként lássunk egy hétköznapi szituációt. A lakás egyik helyisége 3,1 m-szer 4,2 m alapterületű. Ezt négyzet alakú csempékkel szeretnénk kirakni, de lehetőleg úgy, hogy a csempéket ne kelljen darabolni. Ha cm-ben mérve csak egész oldalhosszúságú csempék kaphatók, és szeretnénk a lehető legkevesebb csempét felhasználni, akkor milyen méretűvel oldható meg a feladat? (Az egyszerűség kedvéért tekintsünk el a fugázásból adódó méretkülönbségtől, ...

Láttuk, hogy a természetes számok felépíthetők egymásból, illetve lényegében 1-esekből is, az összeadás művelettel. Az összes lehetséges előállítás, azaz a partíciószám meghatározása viszont komoly kihívás. Mi történik vajon, ha az összeadást egy másik műveletre cseréljük?

Ezúttal is érdekes, de alapvetően más jellegű eredményekhez jutunk, ha összeadás helyett szorzással próbálunk meg számokat „gyártani”. A korábbiakhoz hasonlóan, ...