Amikor az oszthatósági szabályokat tárgyaljuk, a 7-eshez érve gyakran elhangzik, hogy van rá szabály, de túl komplikált, ezért inkább nem is foglalkozunk vele, letudjuk a dolgot ennyivel. Ennek a bejegyzésnek a témája e „rejtély” feltárása lesz.

A közepébe vágva, egy szám akkor osztható 7-tel, ha számjegyeket hátulról hármasával csoportosítva majd váltakozó előjellel összeadva, a kapott eredmény 7-tel osztható. Például az 1 638 763 osztható 7-tel, mert 763 – 638 + 001 = 126, ami két 7-tel osztható szám, a 70 és az 56 összege, tehát osztható 7-tel.

Van egy másik szabály is. Vegyük azt a számot, amit úgy kapunk, hogy az eredeti számunkból töröljük az utolsó számjegyet. Vonjuk ki ebből az utolsó jegy kétszeresét. Ha így egy 7-tel osztható számot kapunk, akkor az eredeti szám is 7-tel osztható lesz.

Például, a fenti 126 esetén 12-2·6=0, ami osztható 7-tel. Egy másik példa, a 8638 esetén 863 – 2·8 = 847. Ezen ránézésre nem látszik, hogy 7-tel osztható-e, de ugyanezzel a módszerrel vizsgálható. Azaz, 84 – 2·7 = 70, ami 7-tel osztható.

Végezetül, a fenti 1 638 763-as példa esetén is működik a módszer: 163 876 – 2·3 = 163 870. Ezt tovább vizsgálva 16 387 - 2·0 = 16 387, majd 1638 – 2·7 = 1624, így 162 – 2·4 = 154, végül 15 – 2·4 =7, ami osztható 7-tel.

Érezhető, hogy a második módszer nagyobb számok esetén nehézkesebb, de kis számoknál remekül használható. A kérdés persze az, hogy mi is e misztikus szabályok magyarázata.

1001 éjszaka, avagy az első módszer indoklása

Az első változat magyarázata igazán mesésen indul, a kulcs ugyanis az 1001-ben rejlik. Egész pontosan abban a tényben, hogy az 1001 osztható 7-tel (143·7). De miért is lényeges ez? Valójában nem az 1001 a fontos számunkra, hanem az 1000, illetve annak hatványai, mivel a 10-es számrendszerben ez az egyik helyiérték. Ha az 1000-et elosztjuk 7-tel az osztási maradék 6, más megközelítésben (-1) lesz: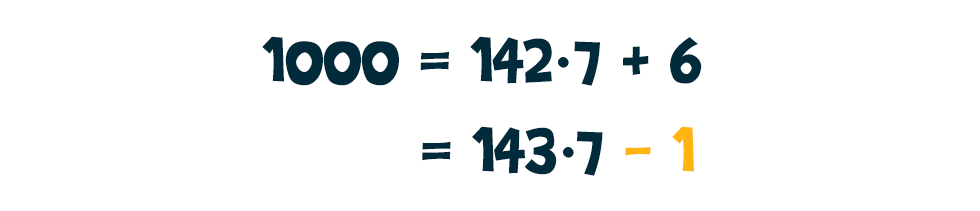A számjegyek hármasával való csoportosítása lényegében megfelel az 1000 hatványaira való felbontásnak (más szóval 1000-es számrendszerben számolunk.). Azaz például az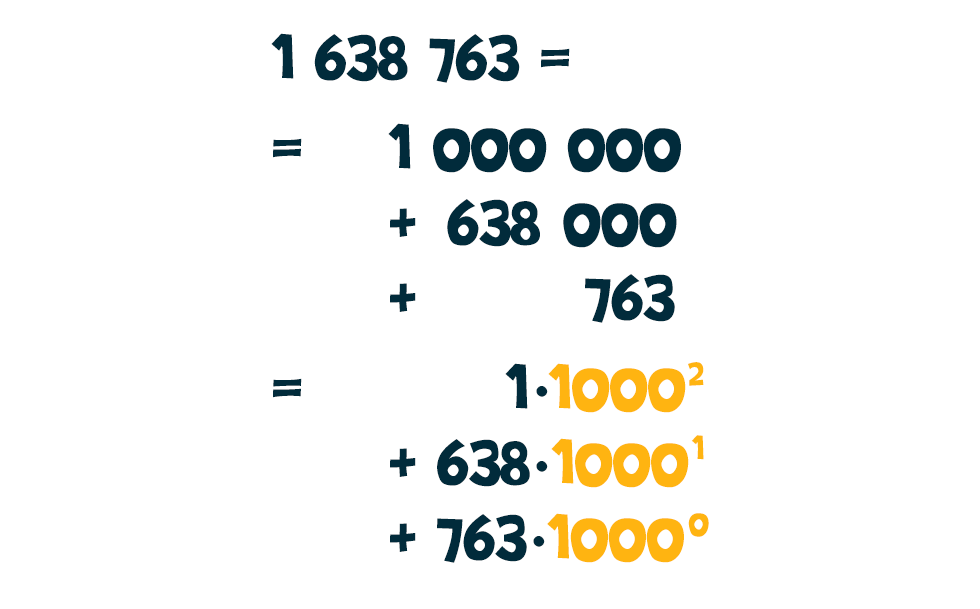Az 1000-nek a 7-tel vett osztási maradéka (-1), az 1000 hatványozása során pedig ezek a maradékok szorzódnak össze, és határozzák meg a szorzat 7-tel vett osztási maradékát. Azaz például az 1000² esetén az első két tag osztható 7-tel, tehát a maradék a harmadik tagból kapható meg, ami esetünkben 1: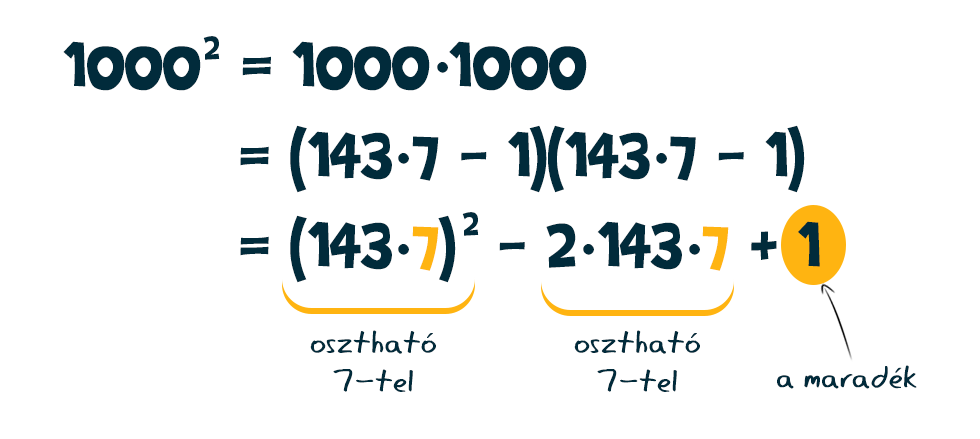Hasonlóan vezethető le, hogy az 1000³-nál a maradék ismét (-1). Folytathatjuk ezt a sort, a negyedik hatványra ismét (+1), az ötödikre (-1) stb. maradékokat kapunk. Más szóval, a maradékok a hatványkitevő növelésével váltakozva (+1) és (-1)-ek lesznek úgy, hogy páros kitevő esetén (+1), páratlan esetén (-1) adódik.

Számolnunk kell viszont természetesen a szorzókkal is, azaz hogy az egyes 1000 hatványokból hány is van. A szorzás az osztási maradékot is szorozza, így például a 638·1000 esetén a maradék 638. Persze ebből levonhatók a kerek egész 7-esek, esetünkben 91-szer 7, így a maradék 1, de ez részletkérdés. A lényeg, hogy ha az egyes 1000-hatványok adott számszorosait vesszük, akkor mindig az adott szám (+1) vagy (-1)-szeresét kapjuk, ráadásul hátulról indulva épp váltakozva. Ezeket összeadva megkapjuk az eredeti számunk 7-tel való osztási maradékát. Ha ez egy 7-tel osztható szám, akkor az eredeti szám is osztható lesz 7-tel. Ha nem, akkor az eredeti sem.

Ezek alapján, az 1638 763-nak a 7-tel vett osztási maradékát úgy kapjuk, hogy 763-szor vesszük a +1-et, 638-szor a (-1)-et és 1-szer ismét a (+1)-et:Ez viszont lényegében épp azt jelenti, hogy a hármas csoportok számait váltakozó előjellel összeadjuk:A szabály általánosságban is hasonlóan vezethető le, a bizonyítás e verzióját éppen ezért mellőzzük, viszont érdekességképpen kongruenciák segítségével illusztráljuk azt.

Kiindulva tehát abból, hogy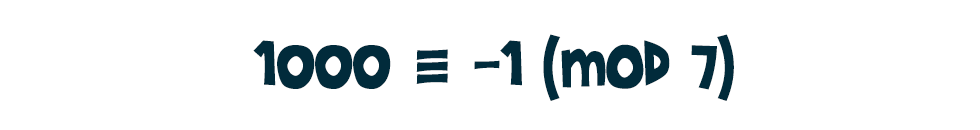a kongruenciák és a hatványozás közti kapcsolat alapján: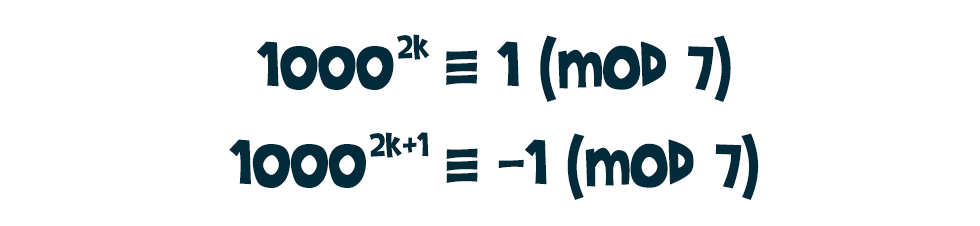Így viszont bármilyen egész c konstansra: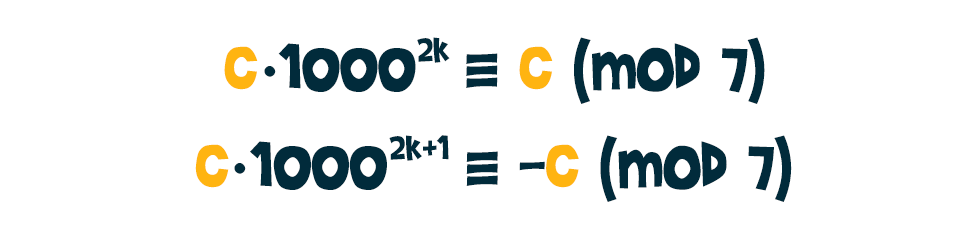Tehát ha n = c₀·1000⁰ + c₁·1000¹ +…+ c_k·1000^k alakú, ahol a c_i-k épp a hármas tagolásból kapott számok, akkor kihasználva a kongruenciák és az összeadás közti tulajdonságot:
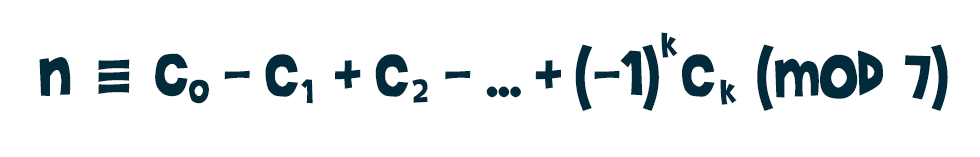Más szóval n pontosan akkor osztható 7-tel, ha a jobb oldal is az.

A másik módszer magyarázata

A dolog alapja itt is hasonló. Az utolsó számjegy leválasztása lényegében azt jelenti, hogy az eredeti számot felbontjuk egy 10-zel osztható és egy egyjegyű szám összegére, azazAz állítás szerint n pontosan akkor osztható 7-tel, ha a „levágott” szám, azaz k és az utolsó jegy kétszeresének, azaz a 2·r-nek a különbsége osztható 7-tel: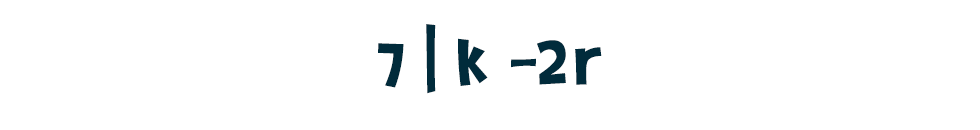Tekintsük kiindulópontnak, hogy n osztható 7-tel. Ekkor n = 7m alakú valamilyen m egész számra, így 10k+r = 7m is fennáll. Most következik egy trükkös lépés, vonjunk ki mindkét oldalból 21·r-t, így a bal oldalon 10, a jobb oldalon pedig 7 emelhető ki, ráadásul a bal oldalon megjelenik az ominózus k-2r kifejezés is: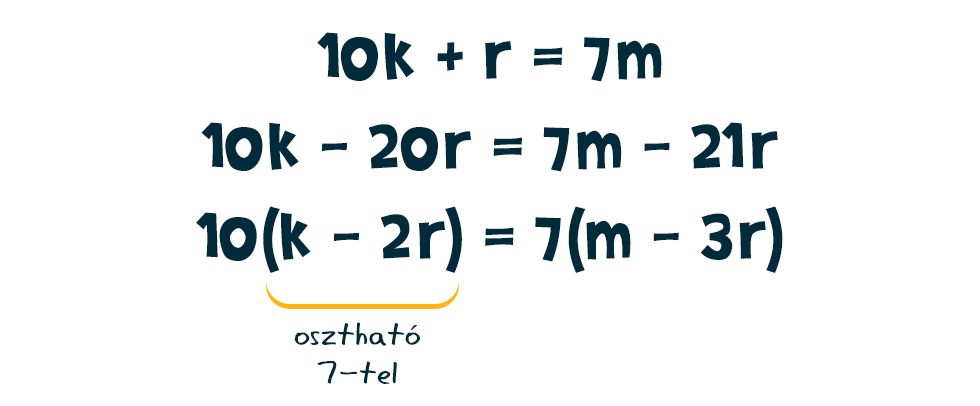Innen már könnyű a dolgunk. A jobb oldal osztható 7-tel, hiszen 7-szer valamilyen egész szám alakú, emiatt a bal oldal is osztható kell, legyen. Na, de a 10 biztosan nem az, így a k-2r-nek kell annak lennie, ami épp az, amit kapni szerettünk volna.

Ezzel viszont még csak az egyik irányú következtetés helyességét igazoltuk, lássuk fordítva is. Tegyük fel ezúttal, hogy k-2r egy 7-tel osztható szám. Ekkor persze a 10-szerese is az, vagyis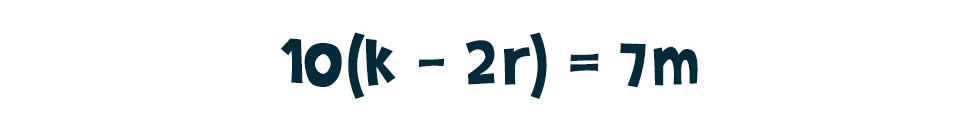alakú. Felbontva a zárójelet, majd hozzáadva mindkét oldalhoz ismét a varázslatos 21·r-t a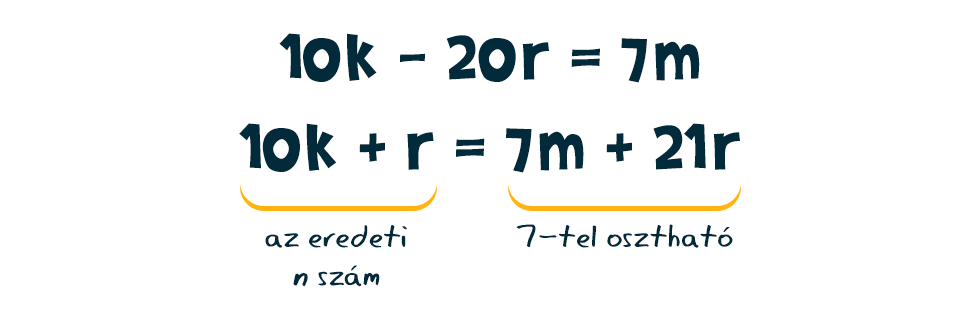egyenlethez jutunk. A bal oldalon így épp az eredeti n számot kapjuk, a jobb oldal pedig két 7-tel osztható szám összege, így a bal oldal is osztható 7-tel: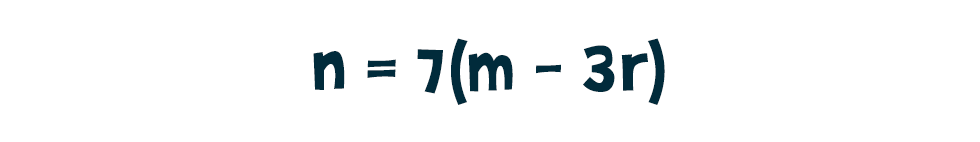Ezzel igazoltuk az állítást.

Források

https://hu.wikipedia.org/wiki/Oszthat%C3%B3s%C3%A1gi_szab%C3%A1lyok

http://mathandmultimedia.com/2012/02/29/divisibility-by-7-and-its-proof/