Kezdésként lássunk egy hétköznapi szituációt. A lakás egyik helyisége 3,1 m-szer 4,2 m alapterületű. Ezt négyzet alakú csempékkel szeretnénk kirakni, de lehetőleg úgy, hogy a csempéket ne kelljen darabolni. Ha cm-ben mérve csak egész oldalhosszúságú csempék kaphatók, és szeretnénk a lehető legkevesebb csempét felhasználni, akkor milyen méretűvel oldható meg a feladat? (Az egyszerűség kedvéért tekintsünk el a fugázásból adódó méretkülönbségtől, hisz a feladat ezzel kalkulálva sem lenne érdemben nehezebb.)A megoldás első lépéseként rögtön váltsuk át cm-be az adatokat. Így lényegében akkor olyan oldalhossz kellene, ami az egyik irányban a 310 cm-t, a másikban a 420 cm-t tökéletesen kiadja. Más szóval olyan számok jöhetnek szóba, amik osztói mindkét számnak. Ilyenek az 1, 2, 5 és a 10. Ha a lehető legkevesebb csempével akarjuk megoldani a problémát, akkor a lehető legnagyobb méretűeket kell választani, azaz a 10 cm-eseket. Ez a feladat nem másról szólt, mint a 310 és a 420 legnagyobb közös osztójának megkereséséről.

Lássunk egy másik példát. Három barátnő teniszezni jár, mindhárman délután 4 órától, de nem feltétlenül azonos napokon. Ha Juli 4 naponta jár le a teniszklubba, Kata minden kedden (azaz 7 naponta), míg Kriszti minden második napon, akkor milyen időközönként találkoznak? Ez a feladat lényegében azt kérdezi, hogy milyen számokban van meg a 4, a 7 és a 2 egyszerre. Sok ilyet tudunk mondani, például a 28, 56, 84 stb. Észrevehetjük viszont, hogy ezek mindegyike a legkisebbnek, azaz a 28-nak a többszöröse. Más szóval, a lányok 28 naponként fognak találkozni a klubban. A megoldás a 4, 7, 2 úgynevezett legkisebb közös többszöröse.

A legnagyobb közös osztó és a legkisebb közös többszörös is a számelmélet alapvető fogalmai közé tartoznak. Technikai szempontból előbbi főként a törtek egyszerűsítésekor kap szerepet, de magasabb szinteken – például kongruenciák megoldhatóságánál vagy számelméleti függvények bizonyos tulajdonságainál – is alapvető fontossággal bír. Utóbbi leginkább a törtek közös nevezőjének meghatározása kapcsán lehet ismerős, de szintén vannak magasabb szintű alkalmazásai is.

LNKO

Két vagy több szám legnagyobb közös osztója, ahogy a neve is mondja, a számok közös osztói közül a legnagyobb. Például a 12, a 20 és a 28 legnagyobb közös osztója a 4, mivel osztója mindhárom számnak, de nincs nála nagyobb közös osztójuk.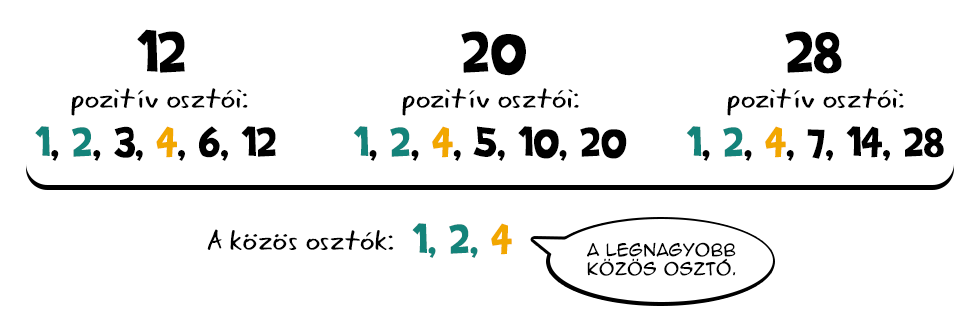A legnagyobb közös osztó meghatározása többféleképpen is történhet, de ha rendelkezésünkre állnak a számok prímtényezős felbontásai, akkor igen egyszerű feladat.

Közös osztók

Először is azt kell észrevennünk, hogy bármely pozitív szám bármely osztója csak ugyanolyan és legfeljebb ugyanakkora kitevőjű prímekből épülhet fel, mint maga a szám. Azaz például, a 360=2³·3²·5 osztói csak 2, 3 vagy 5 prímtényezőkből állhatnak (nem muszáj persze mindnek szerepelnie) és ezek is legfeljebb a 360 előállításában szereplő hatványaikon szerepelhetnek.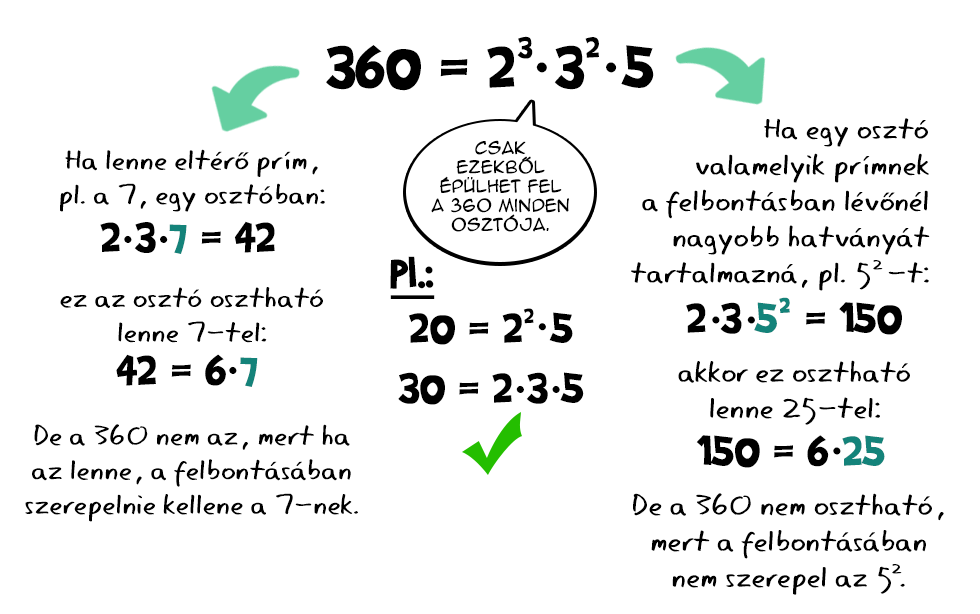Ezek alapján, amikor több szám közös osztóit keressük, akkor azokat is az adott számok prímtényezős felbontásaiból kell összeraknunk méghozzá ugyanilyen módon, azaz csak a közös tényezőket vehetjük figyelembe, és azokat is az előforduló legkisebb kitevővel.

Például, ha a 84 és a 30 közös osztóira vadászunk, az 5-öt nem használhatjuk, mert a 84 felbontásában nincs 5-ös, azaz a 84 nem osztható 5-tel, a 30 hiába igen (a 7 esete hasonló). De egyik közös osztó sem tartalmazhatja a 2²-t sem, hiszen a 30 felbontása csak egy 2-est tartalmaz, más szóval a 30 nem osztható 2²-nal. A 2 és a 3 minden legfeljebb első kitevőjű hatványa viszont szerepelhet minden lehetséges kombinációban, így összesen négy közös pozitív osztót találunk.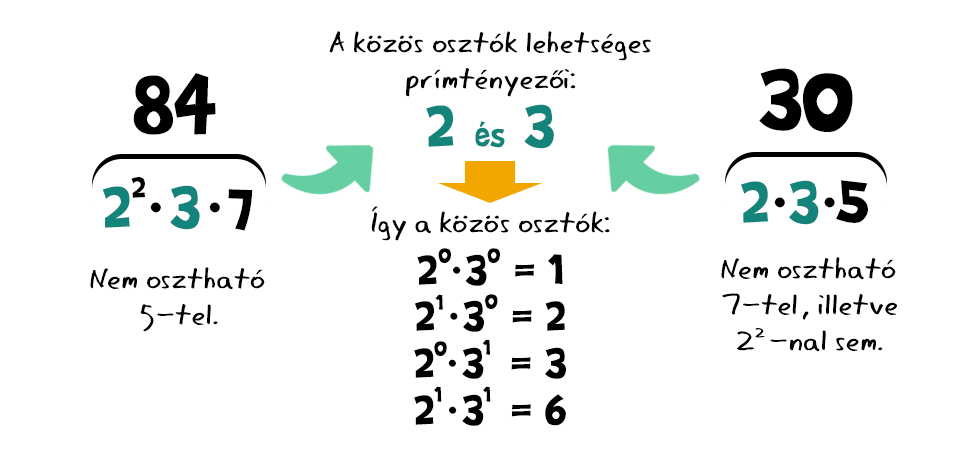

A legnagyobb közös osztó

A legnagyobb közös osztó innen már csak egy apró lépés. A fentieken annyit kell csupán módosítani, mivel a közös osztók legnagyobbikát keressük, hogy nem hagyhatunk ki egyetlen közös tényezőt sem.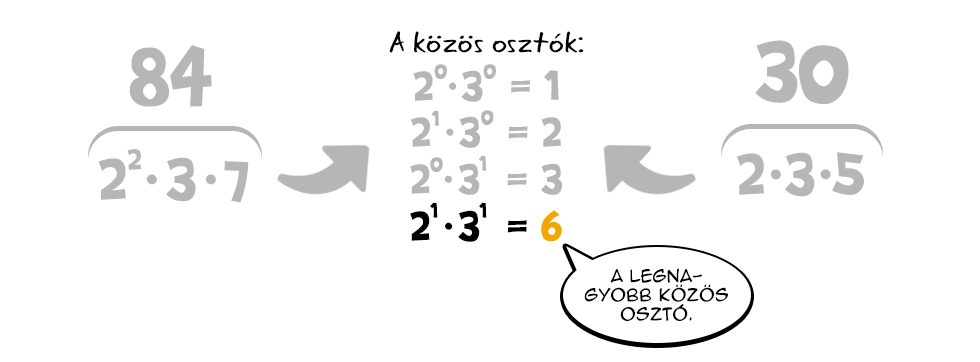Van azonban egy probléma. Mi a helyzet akkor, ha a számainknak nincs egy közös prímtényezője sem? Ekkor nem létezik a legnagyobb közös osztó? Sőt, nincsenek is közös osztóik? A válasz, hogy legalább egy közös osztó mindig létezik, ugyanis az 1 minden számnak osztója, így ebben az esetben ő lesz a legnagyobb közös osztó is. Ezt egyébként felfoghatjuk úgy is, hogy minden prímtényezőből 0 darab közös van, így azok 0-dik hatványainak szorzata (tehát 1) lesz a legnagyobb közös osztó.

Közös többszörösök

Fordítsuk meg a felállást. A közös osztók esetén olyan számokról beszéltünk, melyek osztói a megadott számoknak. Közös többszörösök esetén viszont fordul a kocka, olyan számokat keresünk, melyek az adott számok többszörösei, azaz amiknek az eredeti számaink osztói. (A legkisebb közös többszörös ezek legkisebbike lesz.)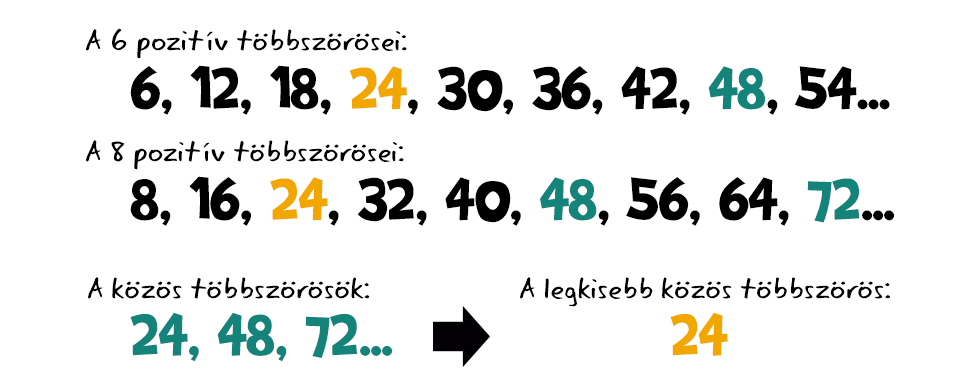

Ez egyfelől azt jelenti, hogy az adott számok prímfelbontásainak egy az egyben megtalálhatónak kell lenniük a közös többszöröseik felbontásában is. Például a 6=2·3 és a 8=2³ esetén nem elég csak egy vagy két 2-est választani, mert a 2·3=6 vagy a 2²·3=12 nem többszörösei a 8-nak.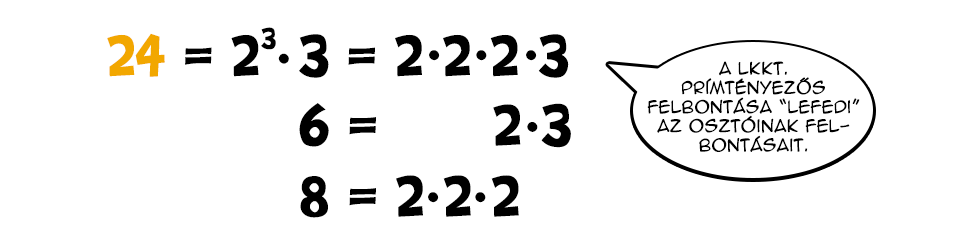Szerepelhet viszont egy közös többszörösben olyan prímtényező, ami az eredeti számaink felbontásaiban nem, hiszen az "extra" szorzó ellenére az még többszöröse marad a megadott számoknak. Például a 6-nak és a 8-nak a 120, a 168, a 264 stb. mind-mind közös többszörösei annak ellenére, hogy tartalmaznak 2-től és 3-tól eltérő prímtényezőt is.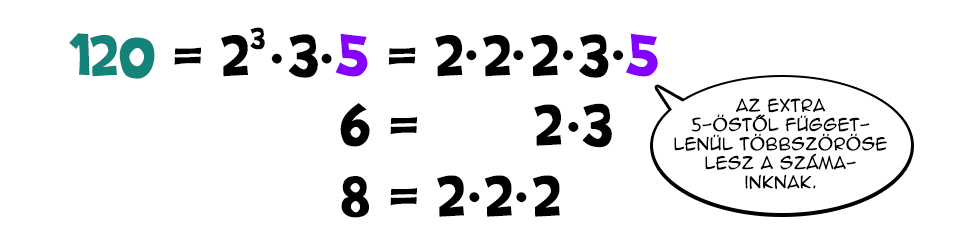Ilyen alapon viszont közös többszörösökből mindig végtelen sok van, így van tehát létjogosultsága annak, hogy a közös többszörösök közül (a pozitív egészek körében) a legkisebb érdekeljen minket.

A legkisebb közös többszörös

A közös többszörösök közül a legkisebbet akkor kapjuk meg, ha semmiféle, a fent említett „extra” tényezőt nem tartalmaz annak prímfelbontása. Összegezve, vegyük a számaink felbontásaiban szereplő összes prímtényezőt úgy, hogy ezek szorzata mindegyik kiindulási számunkat „lefedje”, azaz többszöröse legyen. Ezzel meg is kapjuk legkisebb közös többszöröst.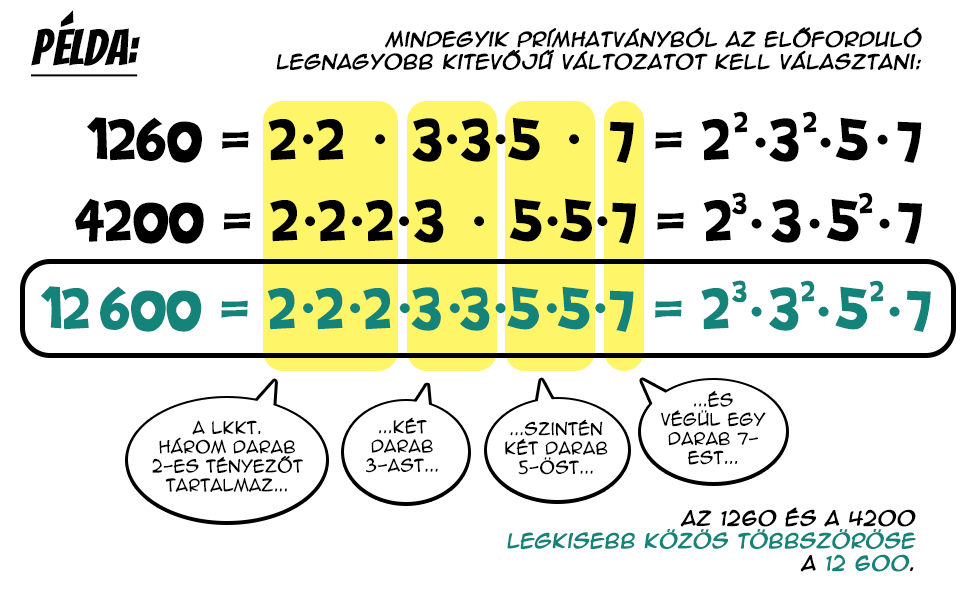 

Kapcsolat

Érdekes kapcsolat vehető észre a legnagyobb közös osztó és a legkisebb közös többszörös, valamint az eredeti számaink között. Ha úgy tekintünk a legnagyobb közös osztóra, hogy az a közös prímtényezők legkisebb kitevős változatainak szorzata, akkor az előállítása során „otthagyott” prímhatványok (amik a közösek nagyobb kitevős hatványai, illetve a nem közös tényezők) szorzata épp a legkisebb közös többszöröst adják.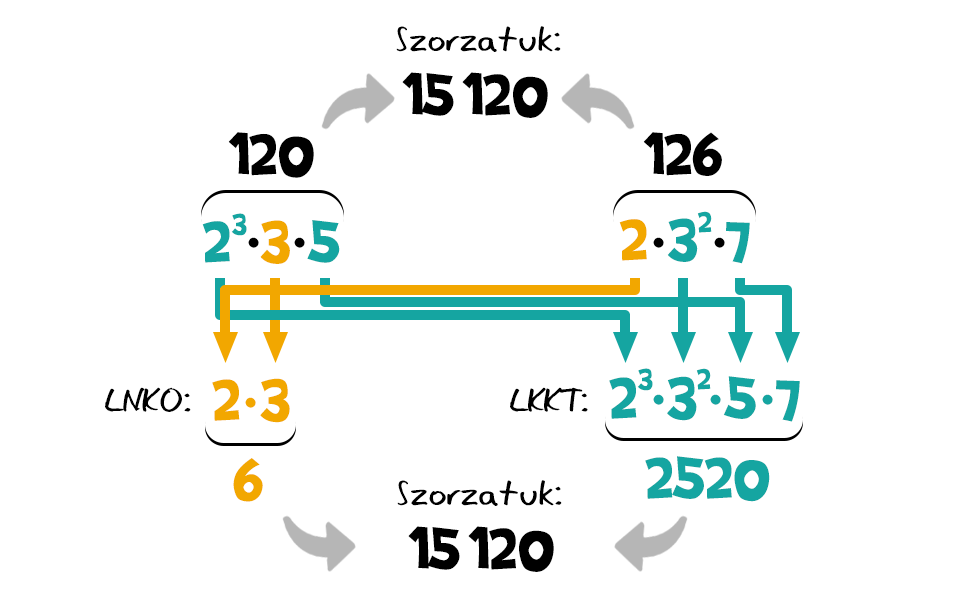Más szóval, két szám legnagyobb közös osztójának és legkisebb közös többszörösének szorzata épp a két eredeti szám szorzata. A dolog szépséghibája, hogy ez kettőnél több szám esetén már nem feltétlenül igaz. Például a 3, 4, 6 legnagyobb közös osztója 1, legkisebb közös többszöröse 12, de ezek szorzata, ami 12, nem egyezik meg a számok szorzatával, ami 72.