Láttuk, hogy a természetes számok felépíthetők egymásból, illetve lényegében 1-esekből is, az összeadás művelettel. Az összes lehetséges előállítás, azaz a partíciószám meghatározása viszont komoly kihívás. Mi történik vajon, ha az összeadást egy másik műveletre cseréljük?

Ezúttal is érdekes, de alapvetően más jellegű eredményekhez jutunk, ha összeadás helyett szorzással próbálunk meg számokat „gyártani”. A korábbiakhoz hasonlóan, miután előállítunk egy adott számot kisebb számok szorzatként, a kapott tényezőket bontsuk továbbiak szorzatára, az így kapottakat szintén stb. Azt fogjuk tapasztalni, hogy ez esetben is van egy határ, ami után az algoritmus érdemben nem folytatható tovább.

Például a 60 esetében 60 = 6·10 = 2·3·2·5. Ha esetleg más felbontással indítanánk, a végén akkor is ugyanoda lyukadnánk ki, csak a sorrend borulna fel kicsit.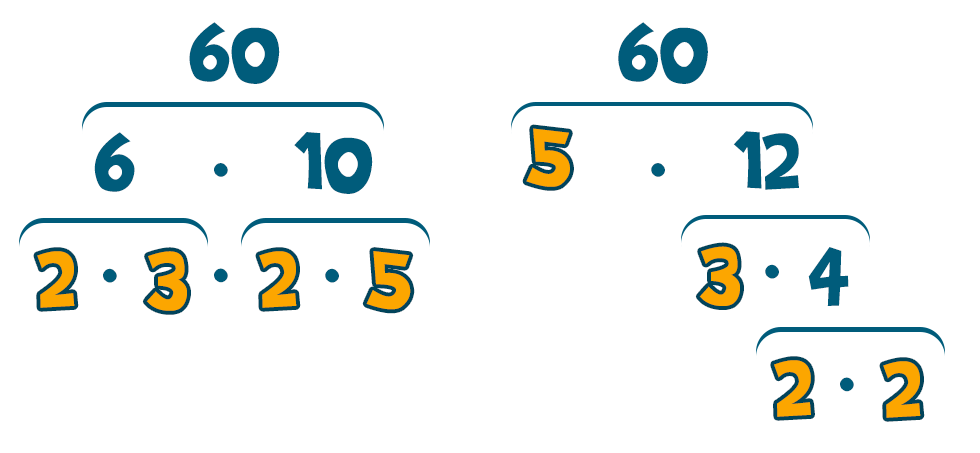A szintet, ahol az eljárás elakad, a prímszámok határozzák meg. Ezek olyan számok, melyeknek pontosan kettő pozitív osztójuk van, saját maguk és az 1, ezért ők már nem bonthatók tovább kisebb (egész) számok szorzatára. (Fontos megemlíteni, hogy az 1 nem prím. Az 1 valójában a prímeknél is különlegesebb szám, de ez egy másik történet.) De egyáltalán mit is jelent az, hogy „osztó”?

Felbonthatóság

Az oszthatóság a számelmélet egyik legalapvetőbb fogalma. Az egyszerűség kedvéért maradjunk a természetes számok (azaz a pozitív egészek és a nulla) körében. Egy természetes szám osztója egy másiknak (vagy ugyanannak), ha létezik olyan, szintén természetes szám, amivel megszorozva épp e másik számot kapjuk.

Bonyolultabbnak hangzik annál, amit takar. Például a 3 osztója a 36-nak, mert létezik olyan természetes szám, nevezetesen a 12, amivel megszorozva épp a 36-ot kapjuk (12·3=36). De fordítva is igaz, a 12 is osztója a 36-nak, mert 3·12=36.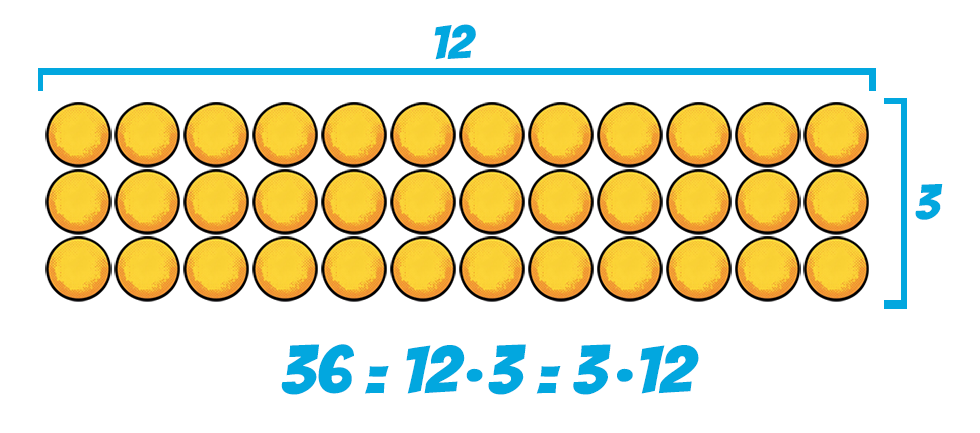Azt is mondhatnánk, hogy ha van 36 labdánk, azt el tudjuk rendezni 12 egyforma hosszú oszlopba, vagy 3, szintén egyforma hosszú sorba is a labdák darabolása nélkül (ez ugye nem lenne túl jó ötlet).

Az osztók egyébként mindig párban járnak, de nem kizárt, hogy egy szám párja saját maga, mint például a 9=3·3 esetében. A teljességhez hozzátartozik még, hogy minden szám osztója saját magának, minden szám osztója a nullának és minden számnak osztója az 1.

Persze a 3·12-nél a 12 tovább bontható lenne 3·4-re, sőt, a 4 is 2·2-re, így végeredményben 36=2·2·3·3, ahol már mindegyik tényező prímszám.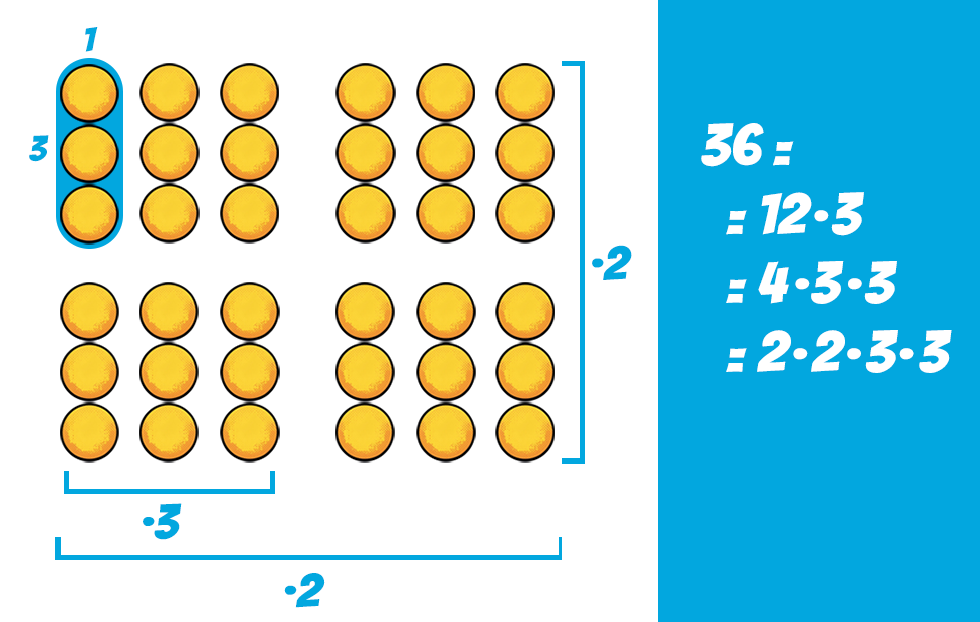
A prímek viszont már csak 1-szer önmagukként lennének tovább bonthatók, amin érezzük, hogy nem egy "valódi" felbontás. Ha a prímek már nem felbonthatóak, természetes, hogy az algoritmusunk ezen a szinten akad el, így az is, hogy (az 1-es mellett) ezek legyenek az építőkockáink.

Prím egyben felbonthatatlan?

Említsük meg ezen a ponton, hogy a prím tulajdonság és a felbonthatatlanság nem egészen ugyanazt jelentik. Általánosságban a prím jelentése az, hogy ha az elem (jelen esetben szám) bármilyen szorzatnak osztója, akkor osztója annak valamelyik tényezőjének is. A felbonthatatlan (más szóval irreducibilis) elem pedig lényegében olyan, aminek csak triviális osztói vannak (ún. egységek, mint pl. az 1 vagy -1, illetve osztójuk persze önmaguk).

Bizonyos algebrai struktúrákban megadható olyan elem, ami irreducibilis, de nem prím vagy fordítva. Példák megadásához tisztázni kellene egy csomó absztrakt algebrai fogalmat, definiálni bennük az oszthatóságot stb., ezért ezen a ponton ezt mellőzzük. De nyugodtak lehetünk, úgynevezett integritástartományokban (mint amilyen az egész számok halmaza is a szokásos összeadás és szorzás művelettel) a prím egyben felbonthatatlant is jelent.

A számelmélet alaptétele

Visszatérve a fő gondolatmenetünkre, két kérdés rögtön adódik. Minden természetes szám felbontható-e prímszámok szorzatára, illetve egy ilyen felbontás egyértelmű-e. A választ mindkettőre a számelmélet alaptétele adja meg.

Maga a tétel azt állítja, hogy bármely 1-nél nagyobb pozitív egész szám a tényezők sorrendjétől eltekintve egyértelműen előáll prímtényezők (vagy prímhatványok) szorzataként.

Bizonyítás: Kezdjük az előállíthatósággal. Az első jelöltünk a 2, ami prím, így nyilvánvalóan felírható 2¹ alakban. Hasonlóan, 3 = 3¹, 4 = 2² stb. (Jegyezzük meg, hogy ugyan a tétel nem szól az 1-ről, de lényegében ez is előállítható bármilyen prímek nulladik hatványainak szorzataként.) Az első néhány szám tehát biztosan felbontható az említett módon.

Tegyük fel ezek után, hogy folytatva a fentieket eljutunk egy bizonyos k számig. Mi a helyzet az ezt következő számmal, azaz a k+1-gyel? Alapvetően két lehetőség van. Lehet, hogy a k+1 is prím, így előáll önmaga első hatványaként, és kész is vagyunk. A másik opció, hogy összetett szám, tehát nem az 1 és nem is prím. Ebben az esetben viszont akkor van önmagánál kisebb (valódi) osztója.

Bontsuk fel hát a számunkat két nála kisebb szám, pl. a és b, szorzatára. (Ne feledjük, a és b egyenlőek is lehetnek, azt ugyanis semmi sem garantálja, hogy k+1-nek egynél több nála kisebb osztója is van – lásd pl. a 9-et.) Mivel ezek legfeljebb akkorák, mint az előző k szám, azaz ameddig a prímfelbontást meg tudtuk csinálni, biztosan előállnak prímek szorzataként. Azonban k+1=a·b, így lényegében a k+1 felbontásakor az a és b felbontásában szereplő prímhatványokat összeszorozhatjuk, ami maga is egy prímfelbontást ad, épp a k+1-ét.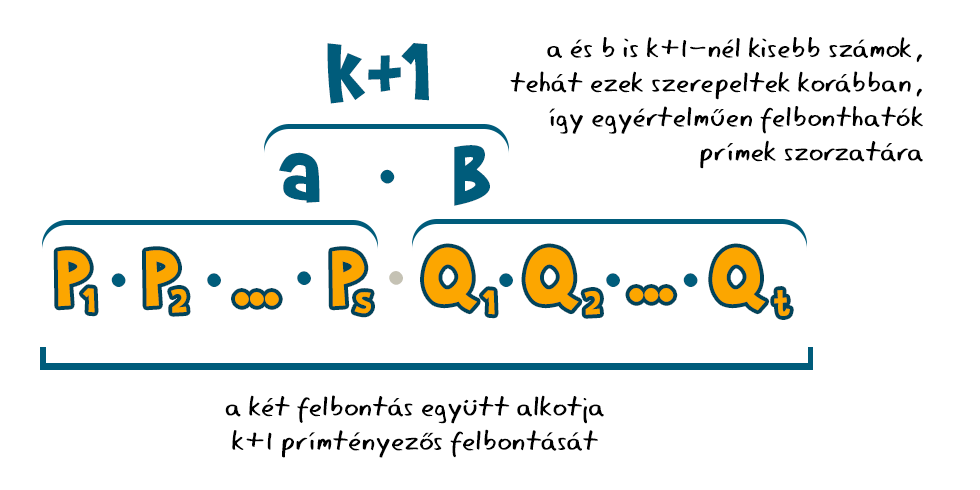Összefoglalva tehát, ha egy bizonyos számig fel tudjuk bontani a számokat prímek szorzatára, és ugyanez mindig megtehető lesz a soron következő számra is, akkor bármelyik számig ellépegethetünk ezzel a módszerrel. Más szóval, ha felbontható a 2, akkor a 3 is, ha a 3, akkor a 4 is, ha a 4, akkor az 5 is, és így tovább. A felbontás létezését tehát igazoltunk bármely természetes szám esetére. (A bizonyítás eddigi részében használt módszer az ún. teljes indukció.)

Lássuk az állítás másik felét. Egyértelmű is egy ilyen felbontás? Tegyük fel, hogy egy adott számnak két, a tényezők sorrendjétől eltekintve is, különböző felbontása létezik: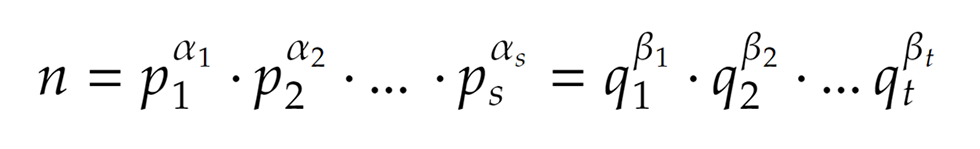Ez akkor azt jelenti, hogy vagy eleve van eltérő prím a felbontásokban, és/vagy valamelyik megegyező tényező kitevője különbözik.

Ha lenne eltérő prím a két felbontásban, akkor a definíció értelmében, mivel ez osztója egy szorzatnak, osztója kell, legyen a másik előállítás valamelyik tényezőjének is, azaz végső soron valamelyik tőle különböző prímnek. Na de egy prím csak 1-gyel és saját magával osztható, a mi prímünk viszont eltérő a másik felbontás összes prímjétől, és definíció szerint nem 1, ez a forgatókönyv tehát kizárt.Marad az a lehetőség, hogy ugyanazok a prímek szerepelnek ugyan a két felbontásban, de legalább az egyik esetén a kitevők különböznek. Ez esetben mindkét szorzatnak oszthatónak kellene lennie az eltérő kitevőjű prím nagyobb kitevős hatványával is, viszont a kisebb kitevős változatot tartalmazó felbontás nem lehet az, ugyanis ebben az adott prímből nincs "elég" példány, és a többi prím sem állhatja elő a hiányzó tényező(ke)t.

Precízebben (az egyszerűség kedvéért koncentráljunk egyetlen eltérésre):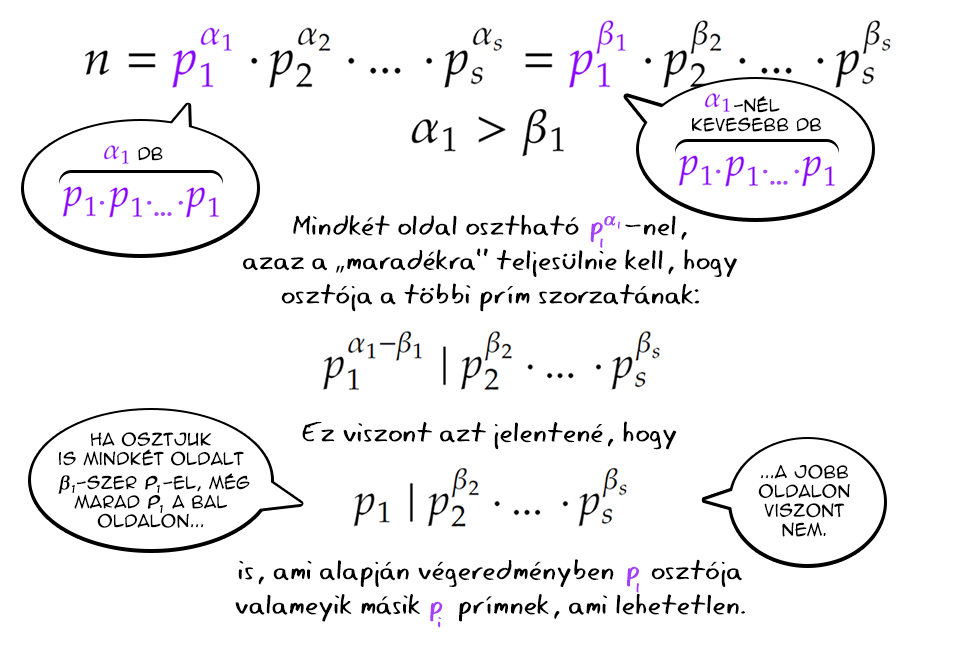

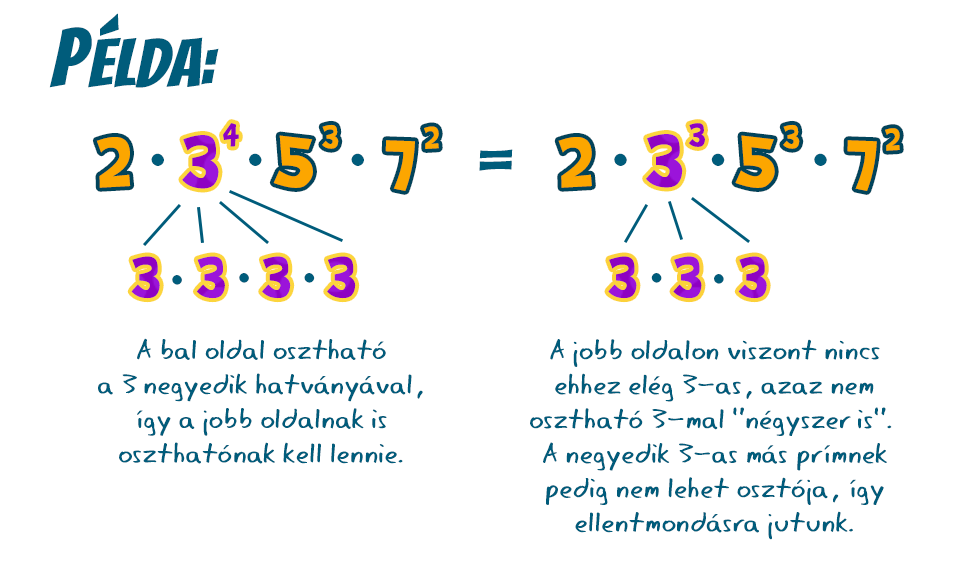Mivel ez a verzió sem lehetséges, csak az az eset marad, hogy a felbontásokban nincsenek eltérő prímtényezők, és az azonos prímek esetén a kitevők megegyeznek, tehát a két felbontás a tényezők sorrendjétől eltekintve tényleg azonos. Ezzel az egyértelműséget is igazoltuk.

Mekkora a készlet?

A fentiek alapján tehát minden pozitív egész előáll prímek szorzataként. Elméletileg ez megvalósítható lehetne véges számú fajta építőelem segítségével is, de nem ez a helyzet, a prímek száma végtelen. Ez nem újkeletű eredmény, már az ókori görög matematikusok is tudták, sőt, mi is az euklideszi bizonyítással indokoljuk.

Az alapgondolat, hogy feltételezzük az állítás hamis voltát, tehát azt, hogy csak véges sok, például 100 darab prímünk van. Legyenek ezek sorba rendezve a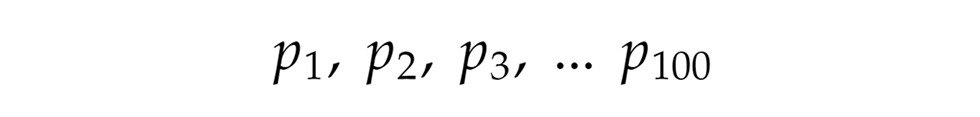A kulcs, hogy kicsit trükkösen alkotunk egy új számot. Szorozzuk össze a fenti prímeket, és adjunk hozzá az eredményhez 1-et: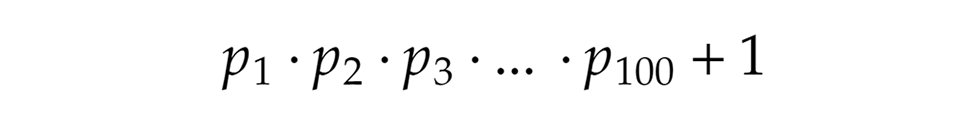Ha ez a szám is prím lenne, az rögtön ellentmondana annak, hogy csak a fenti 100 darab prím van, ez tehát nem lehetséges. Könnyen látható az is, hogy a fenti, általunk alkotott szám nem a 0 és nem is az 1, szükségképpen tehát összetett szám.

Ha viszont összetett, akkor van valódi osztója a fenti prímek között. Jelöljük ezt (vagy egy ilyet) p_i-vel. Ekkor persze, mivel p_i osztója a fenti számnak és egyben a p₁·p₂ ·p₃·…·p₁₀₀ szorzatnak is (hiszen ennek egy tényezője), ezért osztója kell legyen az 1-nek is. Ez viszont szintén nem lehet, hiszen az 1-nek csak önmaga osztója a pozitív egészek körében p_i pedig prím, azaz biztosan nagyobb mint 1.Más lehetőség nem maradt, tehát ellentmondásra jutottunk azzal a feltevésünkkel, hogy csak 100 darab prím létezik. A gondolatmenet tökéletesen ugyanez lenne, bármilyen más számot helyettesítenénk a 100 helyére, azaz az a feltevés sem állja meg a helyét, hogy bármilyen véges számú prím létezik. Más szóval, az eredeti állításnak igaznak kell lennie.

További érdekesség, hogy az is igazolható, hogy két szomszédos prím között akármekkora távolság lehet, azaz a prímek alapvetően ritkák mindamellett, hogy ún. ikerprímpárból (olyan prímekből, melyek különbsége kettő, pl. 5 és 7, 11 és 13, 29 és 31 stb.) viszont végtelen sok van, ami viszont azt jelenti, hogy nem egyszerűen arról van szó, hogy a prímek egyre ritkábban fordulnak elő.

A számok DNS-e

Visszatérve, a számelmélet alaptétele alapján minden pozitív egész számot fel tudunk bontani prímek szorzatára. E felbontás fontos információt hordoz az általa előállított számról. Többek közt meghatározható belőle az adott szám osztóinak száma, azok alakja, vagy akár az osztók összege is. Több szám esetén a felbontás segítségével megkaphatjuk a számok legnagyobb közös osztóját vagy legkisebb közös többszörösét is, melyek összetettebb oszthatósági feladatok megoldásában segédkeznek, de ez már egy másik történet.

Források:

https://www.cuemath.com/numbers/the-fundamental-theorem-of-arithmetic/

Megyesi László: Bevezetés a számelméletbe (Polygon Jegyzettár 1997)