Két szám legnagyobb közös osztójának meghatározása a számok prímtényezős felbontásának birtokában könnyű feladat. Vannak azonban más módszerek is, közülük is a legismertebb talán az euklideszi algoritmus.

Euklidész lemmája

A módszer alapja, hogy bármely két pozitív a és b egész szám esetén egyértelműen létezik olyan nemnegatív q és r egész (ahol fontos, hogy r kisebb b-nél) úgy, hogy: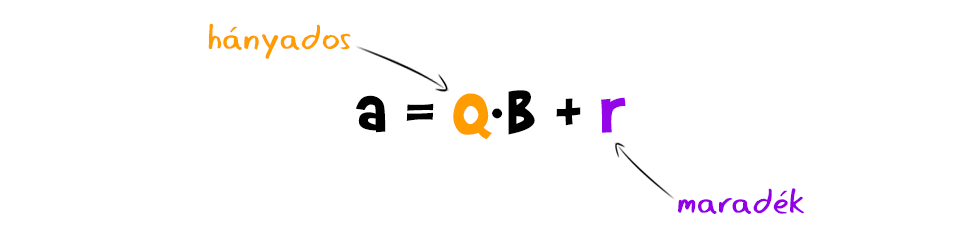azaz az egyik szám (a) előáll a másik (b) valamilyen egész számú (q) többszöröse és egy másik nemnegatív egész (r) összegeként. Például 10 és 23 esetén 23=2·10+3, vagy 10=0·23+10. A q számot hányadosnak, az r-t pedig maradéknak nevezzük. Az első esetben q=2 és r=3, a másodikban q=0, r=10. Ez nem más, mint a jó öreg maradékos osztás.

E jelenség nyilvánvalónak érezhető, de természetesen bizonyítást igényel (a tétel Euklidész osztási lemmájaként is ismert). A precíz levezetést mellőzzük, de lényegében arról van szó, hogy ha a nagyobb számot csökkentjük a kisebb szám pozitív többszöröseivel egészen addig, amíg nem lépünk a 0 alá, akkor ez a folyamat nem folytatható a végtelenségig (a természetes számok alulról való korlátossága miatt.) Az utolsó lépésben kapott szám lesz a maradék, a hányados pedig az eredeti kisebb számnak az a szorzója, ahányszor csökkentettük vele a nagyobb számot.

Például, ha a 23-at csökkentjük a 10 többszöröseivel, akkor 2·10 után akadunk el, mert 23-2·10=3 még nemnegatív, de 23-3·10=-7 már igen. Ez esetben a maradék tehát a 3, a hányados pedig a 2.

Euklidész algoritmusa

Először illusztráljuk az algoritmus működését egy példán. Tegyük fel, hogy keressük a 360 és a 147 legnagyobb közös osztóját. Bármi is ez a szám, mivel osztója mindkettőjüknek, ezért osztója lesz a különbségüknek is. Sőt, ha a 360-ból 2-szer is kivonjuk a 147-et, az így kapott eredménynek, azaz a 66-nak is: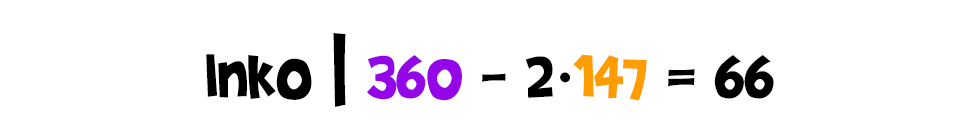Na de, ha osztója a 147-nek és a 66-nak, akkor ezek különbségének is, illetve a 147-2·66 különbségének, azaz a 15-nek is: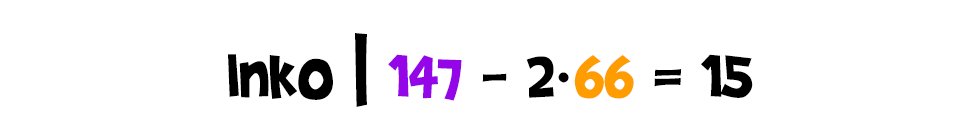Talán már kitalálható, hogy mi lesz a folytatás. 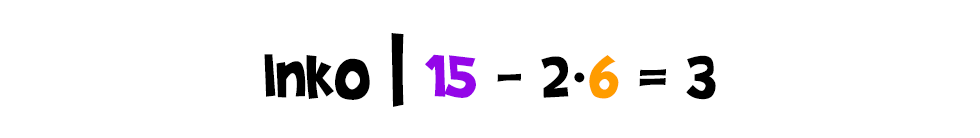A keresett számunk osztója a 66 és a 15 négyszeresének különbségnek is, azaz a 6-nak:Ugyanígy a 15 és a 6 kétszerese különbségének, vagyis a 3-nak is:Végül pedig 6 és a 3 kétszerese különbségének, azaz a nullának is:Mivel a 0-nak minden szám osztója, nem érdemes folytatni az algoritmust.

Az utolsó érdemi információ az utolsó előtti lépésnél keletkezett, nevezetesen, hogy a legnagyobb közös osztó osztója a 3-nak. Pozitív számok körében ez két számot jelenthet, az 1-et és a 3-at. Viszont mivel az utolsó lépés elvégzése során az 1-et átugorjuk, azaz a 0-át kapjuk különbségként, a keresett szám nem lehet osztója az 1-nek, tehát a legnagyobb közös osztó a 3 lesz.

Lényegében a fent látott lépéssorozat az euklideszi algoritmus, de kicsit más formában, átrendezve szokás felírni: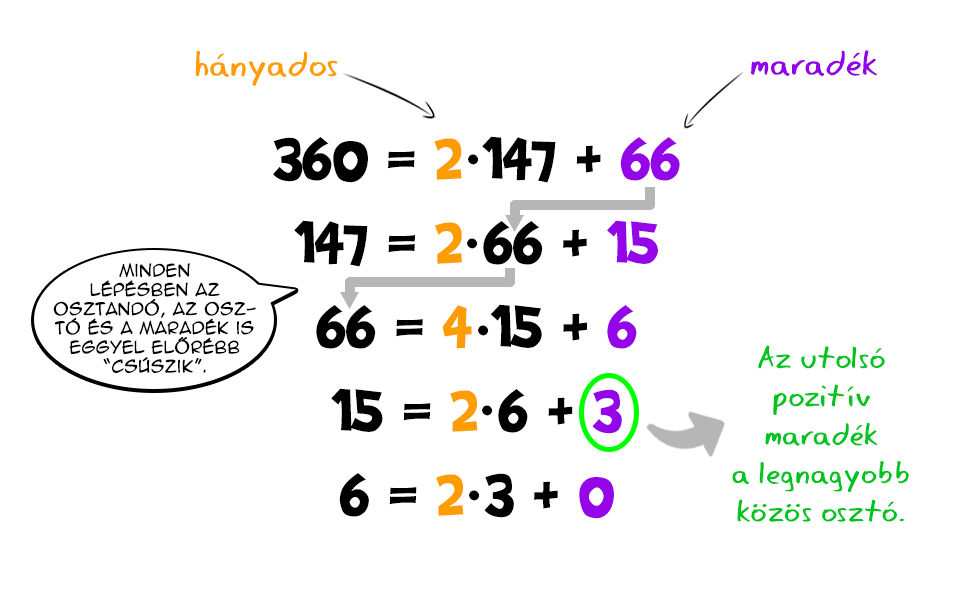Azaz minden lépésben a nagyobb számot állítjuk elő a kisebb szám valahányszorosa plusz valamilyen maradék összegeként, ahol a maradék mindkét eredeti számnál szigorúan kisebb. A legnagyobb közös osztó az utolsó még nem nulla maradék lesz.

Mindezek fényében lássuk, hogyan működik a módszer általános esetben.

A bizonyítás

Legyenek a és b tetszőleges pozitív egészek úgy, hogy b<a. Ekkor a fenti példának megfelelően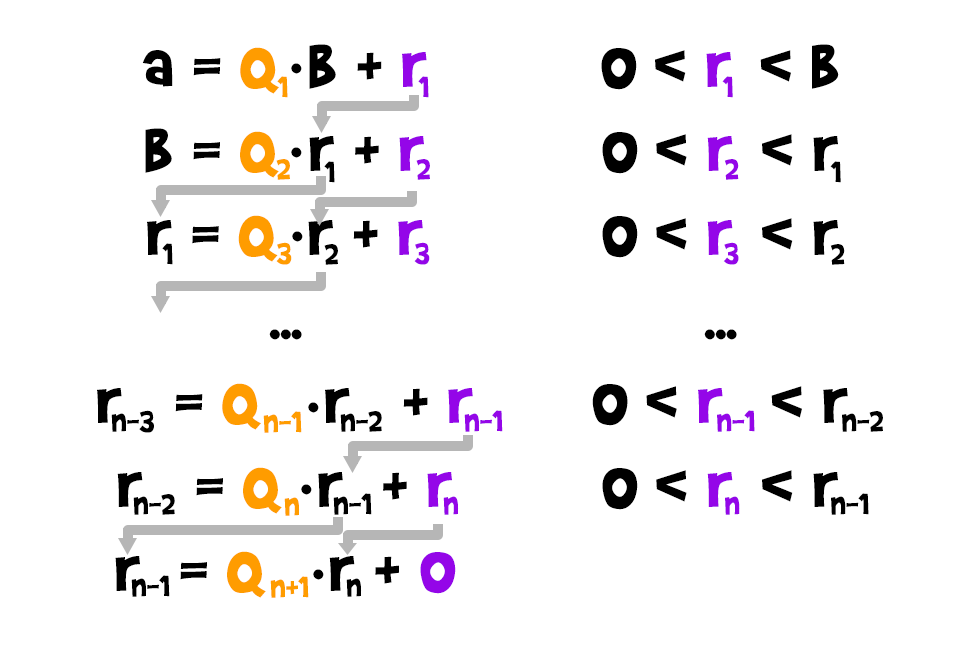Az állítás, hogy ekkor a és b legnagyobb közös osztója r_n.

A bizonyítás során végig kihasználjuk majd azt a tényt, hogy ha egy szám osztója két számnak, akkor az összegüknek is, illetve ha osztója egy kéttagú összegnek és az összeg egyik tagjának, akkor osztója kell, legyen a másik tagnak is. (Pédául, ha a 6 osztója a 30-nak, ami 18+12, és a 6 osztója a 18-nak, akkor a 12-nek is osztójának kell lennie.)

Az utolsó egyenlet alapján r_n osztója r_n-1-nek, mert az q_n+1·r_n-el egyezik meg. Így viszont az utolsó előtti egyenletben r_n egyaránt osztja a jobb oldal mindkét tagját (hiszen osztója r_n-1-nek és saját magának is), ebből következően az összegüket is, ami akkor azt jelenti, hogy a bal oldalt, azaz r_n-2-t is.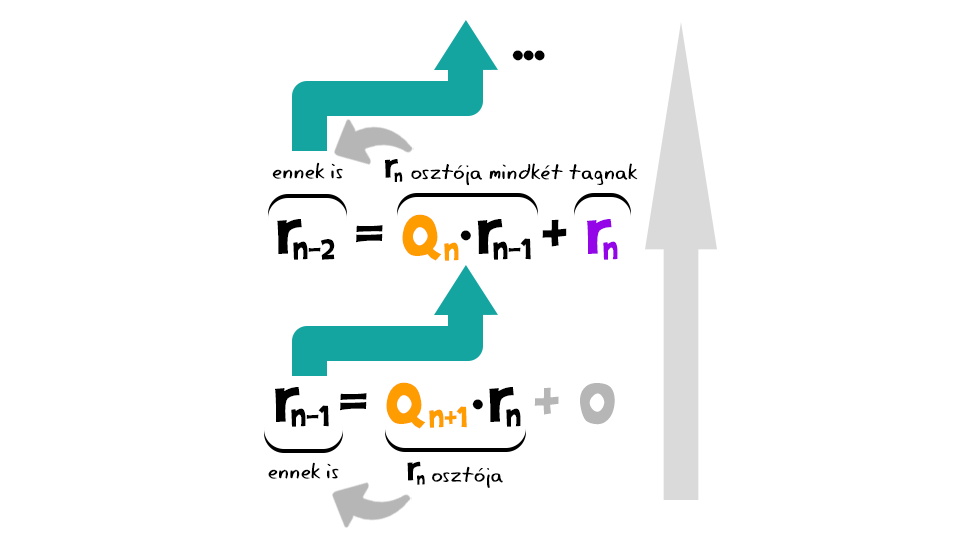Ezt folytatva felfelé, ugyanezzel a logikával eljutunk oda, hogy r_n egyaránt osztója a-nak és b-nek, más szóval közös osztójuk.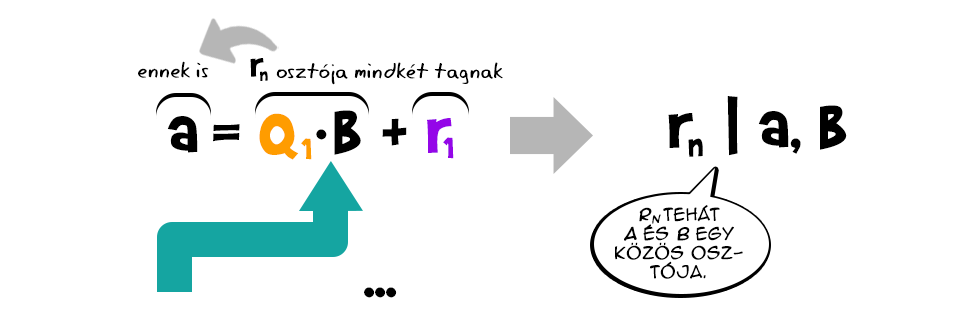Most induljunk el fentről lefelé. Ha egy d szám közös osztója a-nak és b-nek is, az első egyenlet miatt osztója kell, legyen r₁-nek, hiszen a bal oldalnak és a jobb oldal egyik tagjának osztója. Ekkor viszont - hasonló okok miatt - a második egyenlet szerint, mivel b-nek és r₁-nek is osztója, osztania kell r₂-t is, és így tovább, egészen r_n-ig. Végeredményben tehát, a és b összes közös osztójának osztania kell r_n-t, így r_n a két szám legnagyobb közös osztója is egyben.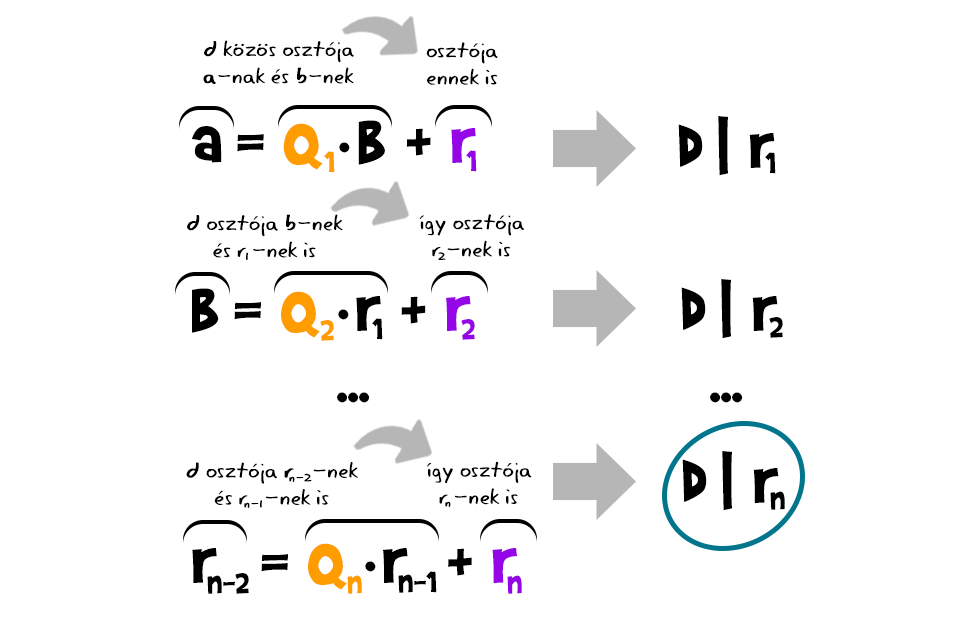

Egyértelműség

A teljesség kedvéért meg kell bizonyosodnunk arról is, hogy a legnagyobb közös osztó egyértelmű-e. A válasz nem teljesen igen, de lássuk a részleteket.

Tételezzük fel, hogy egynél több legnagyobb közös osztó is van, például kettő. Jelöljük ezeket d₁-gyel és d₂-vel. Mivel mindketten legnagyobb közös osztók, a és b összes közös osztója osztója mindkettőnek. Viszont akkor ez egymásra is vonatkozik, azaz d₁ osztója d₂-nek és d₂ is osztója d₁-nek. Ezt a szituációt úgy nevezzük, hogy d₁ és d₂ asszociáltak (mint például a +3 és a -3).

Általában tehát a legnagyobb közös osztó csak asszociáltság erejéig meghatározott, viszont, ha a pozitív egészekre korlátozzuk magunkat (ahogy a fentiekben tettük is), akkor egyértelmű, ugyanis ebben a számkörben minden szám csak önmagával asszociált.

Említsük még meg, hogy ha kettőnél több legnagyobb közös osztót feltételezünk, a bizonyítás akkor is hasonlóan történik, csak miután levezettük az első két legnagyobb közös osztó asszociáltsági viszonyát, akkor az egyiket közülük párba állítjuk a következő legnagyobb közös osztóval stb. A végén azt fogjuk kapni, hogy ezek mind asszociáltak, más szóval egy asszociáltsági osztályba tartoznak. (Pozitív egészek esetén viszont ez lényegében az összes megegyezőségét jelenti.)

A legnagyobb közös osztó előállítása az eredeti számokkal

Az euklideszi algoritmust használva két pozitív egész legnagyobb közös osztója felírható az eredeti számok úgynevezett lineáris kombinációjaként, azaz valahányszor az egyik és valahányszor a másik alakban. Például a 360 és a 147 esetén 3 = 49·147-20·360. Ez úgy kapható meg, ha az algoritmus egyenletein haladva kifejezzük a maradékokat...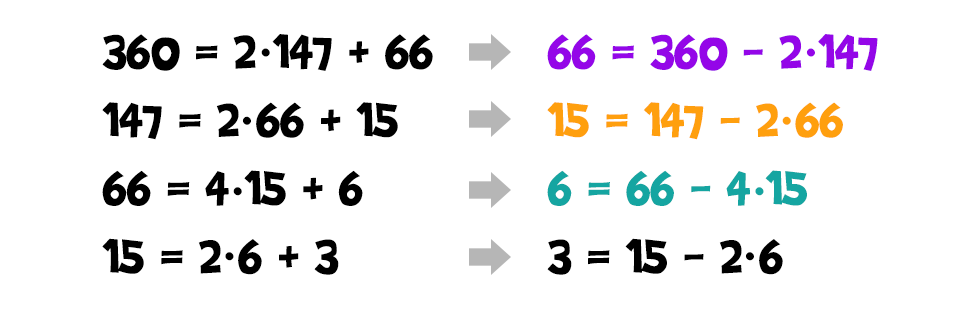...majd a legnagyobb közös osztó felbontásától visszafelé haladva mindig behelyettesítjük a korábbi eredményeket: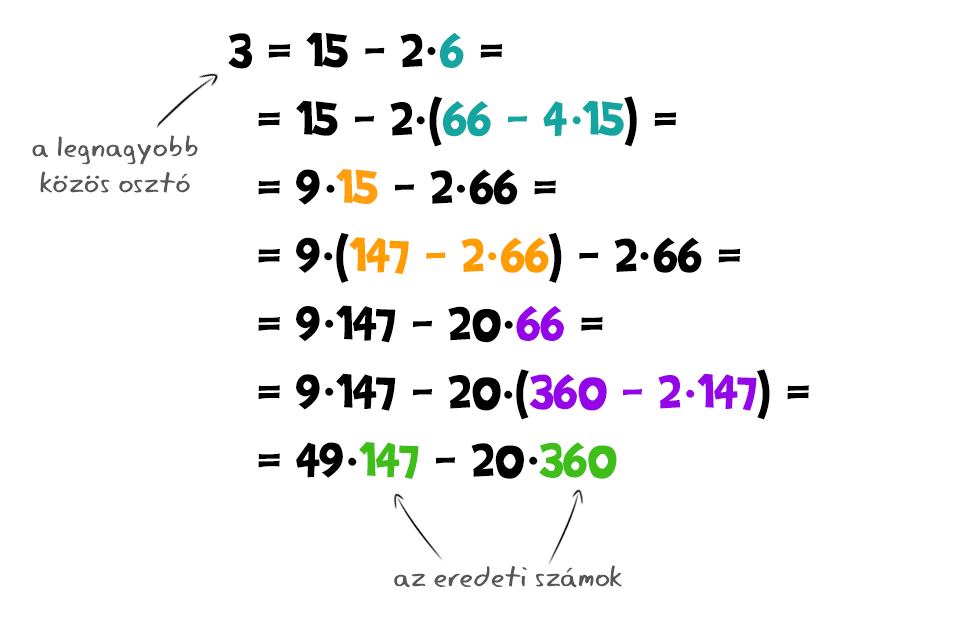Lényegében ez az általános esetben is ugyanígy történik, ennek technikai részleteitől azonban most eltekintünk.

Források:

https://math.hawaii.edu/~pavel/gcd.pdf

https://www.cuemath.com/numbers/euclids-division-lemma/

Megyesi László: Bevezetés a számelméletbe (Polygon Jegyzettár 1997)