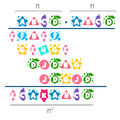
Számokat „építeni” sokféleképpen lehet, mindenképp szükséges azonban hozzá valamilyen építőelem és kötőanyag. Kézenfekvő ötlet lehet, hogy az építőkövek bizonyos számok legyenek, a kötőanyag pedig valamilyen matematikai művelet.

Talán a legegyszerűbb gondolat, ha veszünk egy rakás 1-est és az összeadást. Ekkor pusztán ezek segítségével végtelen sok számot tudunk alkotni. Ha hozzáadjuk az 1-hez önmagát, egy új számot kapunk, a 2-t. Ha ehhez is hozzáadunk 1-et – vagy más szóval, három darab 1-est adunk össze – megint egy új szám keletkezik, a 3, és így tovább. Ha folytatjuk ezt az algoritmust, szép lassan minden pozitív egész számot megkapunk. Flancosabban fogalmazva az 1 generálja a pozitív egész számok halmazát az összeadás segítségével.

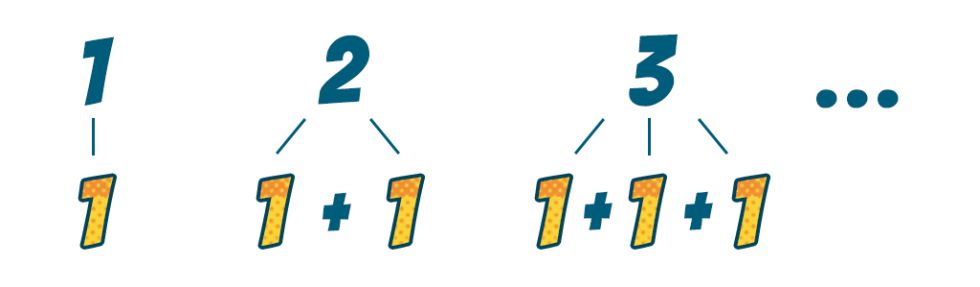Persze gyorsíthatunk is kicsit a dolgok menetén. Nem jelent érdemi változást a végeredmény szempontjából, ha nem egyesével haladnunk, hanem korábbi „blokkok összeragasztásából” kreálunk újabb számokat. Például a 6-ot előállíthatjuk 5+1-ként, 4+2-ként vagy 3+3-ként is, sőt, kettőnél több tag összegeként is, de ha az előállításban résztvevő tagokat tovább bontjuk, végül mindig egy olyan összeghez jutunk, ami csupa 1-esből áll.
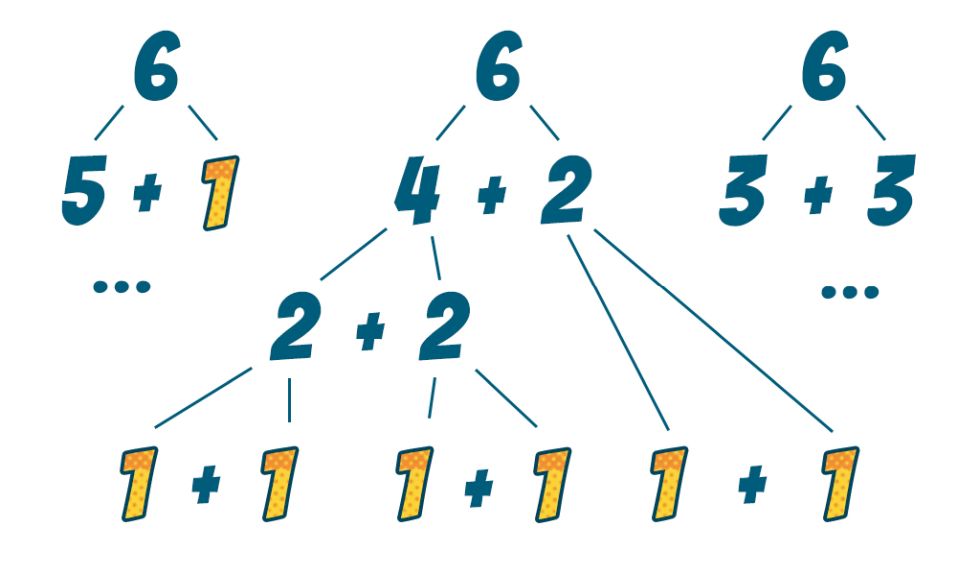Ezzel lényegében végeztünk is, minden pozitív egész szám felépíthető összeadással az értékének megfelelő számú 1-es segítségével. Mindez önmagában nem túl érdekes, de van itt azért még valami.

Partíciók

Egyesek összegeként minden pozitív egész számot csak egyféle módon állíthatunk elő, ez tiszta sor. De vajon hányféle olyan előállításuk létezik, ami nem feltétlenül csak 1-eseket használ? A kérdésre a válasz talán még a vártnál is bonyolultabb. Sőt, ami igazán meglepő lehet, hogy nincs is olyan képlet, ami kapásból választ adna a kérdésre általános esetben. Mielőtt azonban belemennénk a részletekbe, tisztázzuk, miről is van szó.

Egy természetes szám szintén természetes számok összegére való felbontását a szám egy partíciójának nevezzük. Az összegben szereplő tagok sorrendje mellékes, illetve értelemszerűen a 0 az összeadás részeként nem sok vizet zavar, azaz lényegében elég a pozitív számok körében keresgélnünk. A fenti példában tehát az 5+1 vagy az 1+1+1+1+1+1 is a 6 egy-egy partíciója. Jegyezzük meg azért, hogy a 0 is gond nélkül bevonható a felbontandó számok sorába, ezt úgy értelmezzük, hogy 0 darab 1-est használunk. Ezzel együtt megengedjük az egyelemű, triviális felbontást is, azaz például az 1 egyenlő egy darab 1-es „összegével”.

A felbontási lehetőségek, azaz a partíciók számának problémaköre a számelmélet (és legalább annyira a kombinatorika) egy régi és izgalmas kérdése. Kezdetben még könnyű a dolgunk, a 0-nak és az 1-nek például csak egy-egy partíciója van, saját maguk. A 2-nek se sokkal több, az 1+1 és szintén önmaga, azaz a 2. A 3-nak viszont már az 1+1+1, a 2+1 és a 3 is, míg a 4-nek az 1+1+1+1, a 2+1+1, a 3+1, a 2+2 és a 4.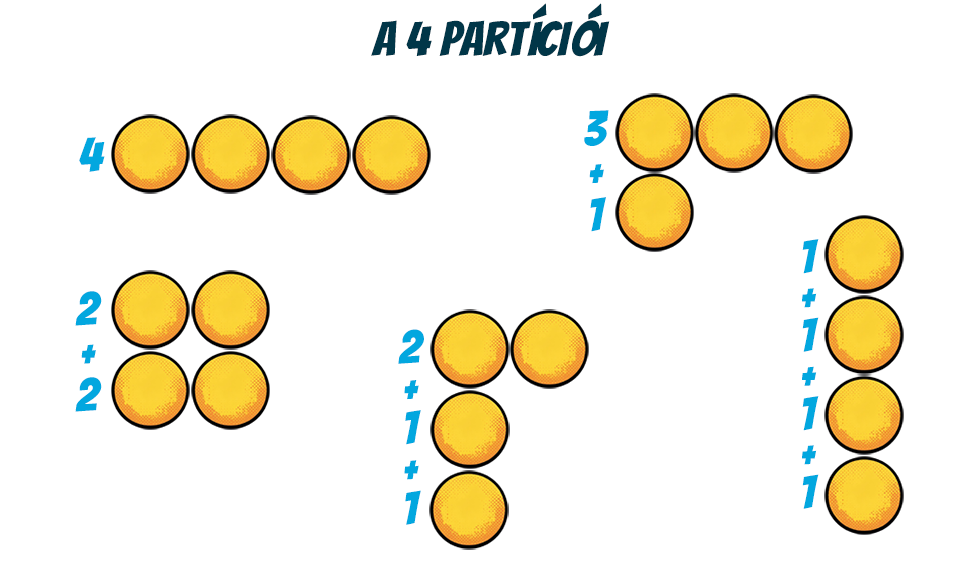A partíciókat általában megfelelően elrendezett pontokkal (Ferrers-diagram, lásd fent) vagy egymáshoz ragasztott, "Tetris" elemekre emlékeztető, négyzetekkel (Young-diagram) ábrázoljuk. Minden egyes pont (vagy négyzet) egy 1-esnek felel meg, például egy három pontot tartalmazó sor a 3-at szimbolizálja. A sorok felülről lefelé rövidülnek, számuk pedig megadja, hogy hány tagból is áll a felbontás.

Az első néhány természetes számot követően gyorsan elkezd növekedni a partíciószám. Sajnos tovább haladva a felírás egyre komplikáltabb, ebből eredendően pedig a partíciók számának meghatározása is egyre nehezebb. Persze azért a helyzet nem teljesen reménytelen.

Volt egyszer egy...

Történetünk valamikor 1674-ben indul, amikor is Gottfried Leibniz egy Jakob Bernoullinak írt levelében azt a kérdést feszegette, hogy a természetes számokat hogyan is lehet szintén természetes számok összegére bontani. (Ugye ismerős?) Leibniz 6-ig meg is válaszolta saját kérdését, majd levonta azt a téves következtetést, hogy a felbontások száma mindig prím (kivéve persze az 1-ét és a 0-ét). Hamar rájött azonban, hogy a kijelentése elhamarkodott volt, ugyanis már a 7 partícióinak száma sem prím, egész pontosan 15.

Az első, aki komolyabban is elmélyült a témában, a rendkívül termékeny svájci matematikus, Leonhard Euler volt. Az ő nevéhez fűződik például az a megfigyelés (és egyben tétel), miszerint egy természetes számnak a csak páratlan számokat tartalmazó partícióinak száma ugyanannyi, mint az olyanoké, amik csupa különböző tagból állnak.

Például a 4 esetén két-két ilyen van: a csupa páratlan tagú partíciók a 3+1 és az 1+1+1+1, míg a különböző tagúak a 3+1 és a triviális partíció, azaz a 4. Említsük meg persze, hogy a két fajta partíció között lehet átfedés, ugye a 3+1 is ilyen.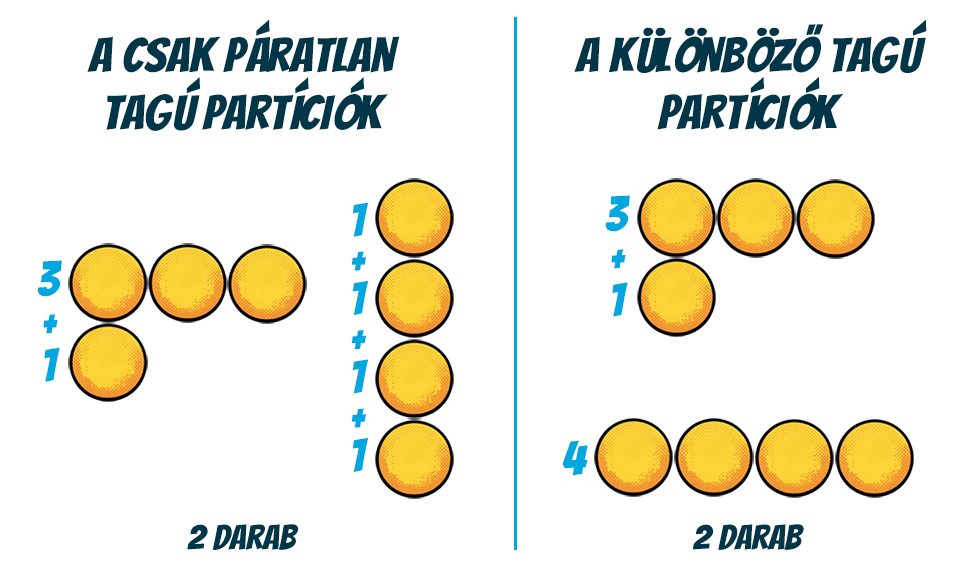Ahhoz azonban, hogy általánosságban is igazolhassuk ezen állítást, meg kell ismerkednünk a szintén Euler által felfedezett, a particiók számára vonatkozó generátorfüggvénnyel.

Egy szárítókötélnyi szám

Először is, a generátorfüggvény (ami igazából egy ún. formális hatványsor) egy kissé csalóka elnevezés, ugyanis nem a megszokott értelemben jelent függvényt. Persze van benne változó (lehet akár több is) műveletek stb., de célját tekintve alapvetően csak a változót tartalmazó különböző tagok együtthatói érdekesek belőle számunkra. Ugyan a könnyebb kezelhetőség érdekében általában egy kompaktabb képletbe szokás sűríteni őket, de ezeket a képleteket sem a függvényeknél megszokott számolásokra használjuk feltétlenül.

Pólya György, világhírű magyar matematikus a generátorfüggvényt egy kis tasakhoz hasonlította, amiben sok kis apróságot (esetünkben számokat) cipelhetünk kényelmesen. De talán Herbert Wilf megfogalmazása még szemléletesebb. Szerinte a generátorfüggvény egy ruhaszárítókötélhez hasonlítható, amire bizonyos számok sorozatát lógatjuk fel.

Ahelyett viszont, hogy elvesznénk a generátorfüggvények világának részleteiben, elégedjünk meg a konkrét esetünkben főszerepet kapó generátorfüggvény koncepciójával és működésének szemléltetésével.

"Tiszta" partíciók

Először is, fordítsuk meg az eddigi alapfelállást. Ne abból induljunk ki, hogy egy adott számot hogyan tudunk felbontani, hanem vizsgáljuk azt a kérdést, hogy bizonyos építőkockákból milyen számokat tudunk előállítani. Az egyszerűség kedvéért ráadásul először tekintsünk csupa egyforma elemet.

Például csak 1-esekből bármilyen pozitív szám, és pontosan egyféleképpen állítható elő, ezt már korábban láttuk. Kódoljuk ezt a következőképpen. Tekintsünk egy olyan végtelen hosszú összeget, amiben a változó olyan hatványai szerepelnek, melyek kitevői mindig eggyel nagyobbak az előzőnél, és induljunk a nulladik hatvánnyal (x⁰ ugye 1).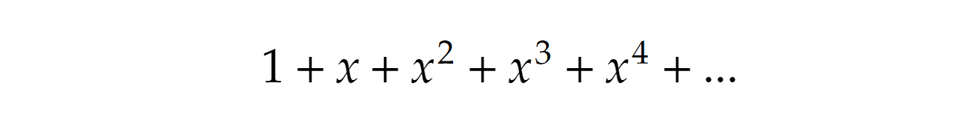Kicsit jobban kidomborítva a lényeget: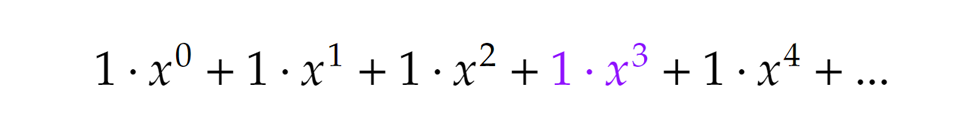Ez a koncepció tökéletes lesz számunkra. A kitevőket megfeleltethetjük a felbontandó számainknak, az együtthatókat pedig annak, hogy az adott szám csak 1-esekből hányféleképpen állítható elő. Például az 1⋅x³ azt takarja, hogy a 3 csak egyféle módon áll elő 1-esek összegeként (3=1+1+1). Talán még szemléletesebb lenne az alábbi alak: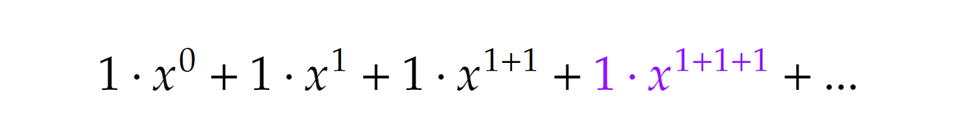Lépjünk tovább. Mi történik, ha 1-esek helyett csak 2-eseket használunk. Ekkor csak páros számokat tudunk alkotni, pl. 2+2=4, 2+2+2=6 stb. Így érdemes ezúttal olyan végtelen összeget (azaz végtelen sort) használnunk, melyben a kitevők kettesével növekednek, hiszen a páratlan számok úgysem (pontosabban 0-féleképpen) állnak elő 2-esek összegeként. Viszont a páros számok csak 2-esekre bontása is egyetlen úton történhet, tehát ezek együtthatói is mind 1-esek lesznek: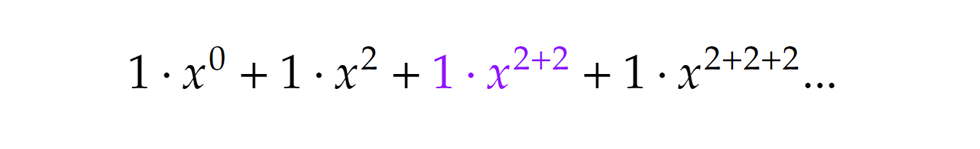Azaz például a 4 csak egyféleképpen áll elő 2-esek összegeként, 2+2-ként. Kicsit egyszerűbben: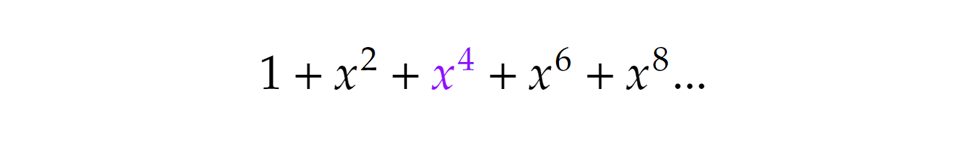Hasonló logika mentén folytathatjuk a sort. Csupa 3-assal csak 3-mal osztható számokat állíthatunk elő, és azokat is csak egyetlen módon, vagyis itt a következő kifejezést kapjuk: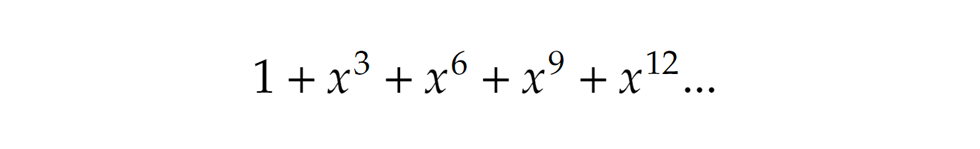csupa 4-es használata esetén pedig az alábbi végtelen összeget: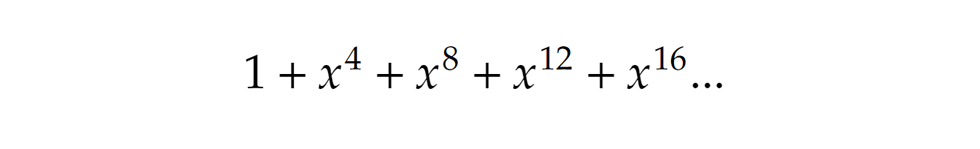…és így tovább. Ezeket a végtelen sorokat hívhatjuk már generátorfüggvényeknek azokban az esetekben, amikor a partíciók csupa azonos tagot tartalmaznak.

"Vegyes" partíciók

Mi a helyzet a vegyes partíciókkal? Egy partíció természetesen tartalmazhat (sőt, legtöbbször tartalmaz is) különböző tagokat is, például 10=1+1+1+2+2+3, ezért általánosságban úgy kell választanunk elemeket, mintha egy svédasztalról válogatnánk össze a reggelinket, innen is kicsit, onnan is kicsit.

Ha például a 10-et a fenti módon akarjuk előállítani, akkor szükségünk lesz három 1-esre. 1-eseket viszont csak az első végtelen összegben használtunk, tehát innen kell választanunk. Emlékszünk még, ugye, hogy a három darab 1-est a szárítókötélen az x³ „tárolja” (3=1+1+1), így ez lesz a választottunk.

Hasonló alapon, a két darab 2-est a második összegből kell beszereznünk (hiszen 2-eseket ott használtunk), amit az ottani x⁴ biztosít (4=2+2). Végül pedig az egy darab 3-ast a harmadik végtelen összegből veszük, ami az ottani x³ választásával valósul meg (3=3). Azaz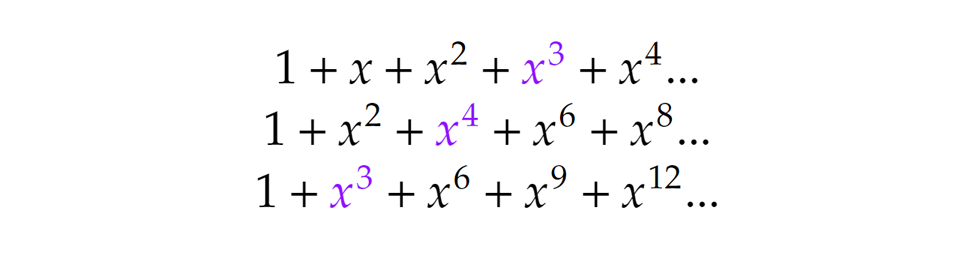Így az 1+1+1+2+2+3 partíció annak a kifejezésnek felel meg, ami a kiemelt hatványok összeszorzásából keletkezik, mivel a felbontandó számaink a kitevőkben ülnek, azokat pedig valamilyen úton-módon, de összeadnunk kellene (ld. az azonos alapú hatványok szorzásának azonosságát).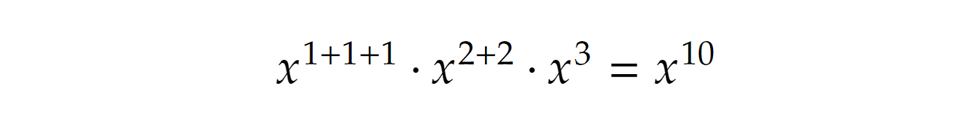Persze ez a 10-nek csak egyetlen partíciója, de hasonlóan építhető fel bármelyik. Az összes lehetséges eset számának meghatározásához ezek alapján össze kell gyűjtenünk az összes olyan kombinációt, melynek eredményeként az x¹⁰ előáll, azzal a megkötéssel persze, hogy minden végtelen összegből csak egy tagot választhatunk.

Sőt, ha kicsit tovább gondoljuk a koncepciót, ilyen alapon minden természetes szám partíciószámát megkaphatjuk. Ha összeszorozzuk a fenti összes (azaz végtelen sok) végtelen összeget, a zárójelfelbontások és az összevonások után az egyes x-hatványok együtthatói épp a kitevőnek megfelelő szám összes előállítási lehetőségével egyeznek meg.

Maradva a 10 példájánál, ha vesszük a végtelen soraink szorzatát, és összegyűjtjük az összes olyan szorzatot, ami x¹⁰-t eredményez, akkor az x¹⁰ együtthatója épp a 10 partícióinak számát adja.

Említsük meg, hogy persze ezzel nem veszítjük el a korábbi, „tiszta” partícióinkat sem. Ugyanis, ha az egyik összegből egy nem 1-es tagot választunk, az összes többiből pedig 1-est, akkor az mindig egy csupa azonos tagból álló partíciónak felel meg.

Az összegek összeszorzásából kapott szintén végtelen összeg lesz az általános eset generátorfüggvénye, ami már a „tiszta” és a „vegyes” partíciókkal egyaránt számol: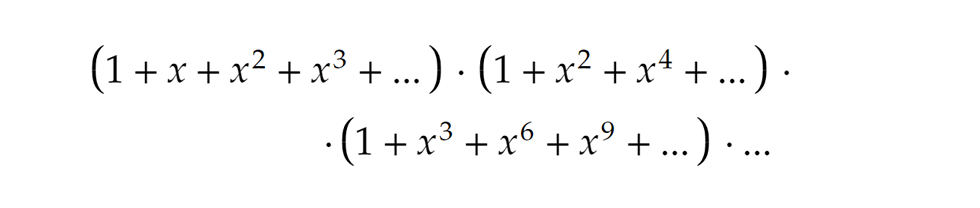Kibontás és összevonás után pedig elég csak megkeresnünk az adott számunknak megfelelő kitevőt, és leolvasnunk a hatvány együtthatóját.

Példa

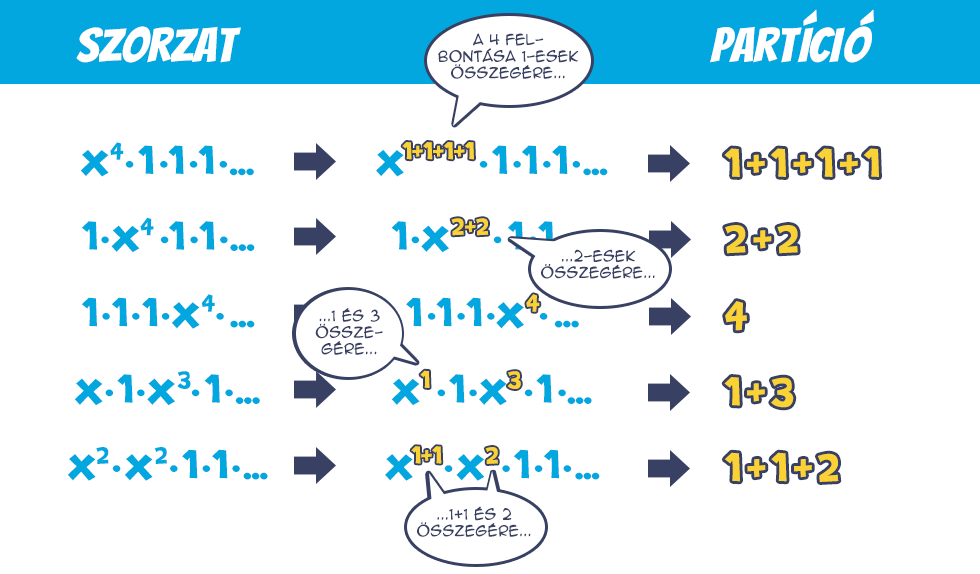
Lássunk még egy példát a jobb érthetőség kedvéért. Térjünk vissza a 4 partícióihoz. Ebben az esetben a generátorfüggvény felírásakor a negyedfokúnál magasabb tagok kiírását mellőzhetjük is, hiszen 4-nél nagyobb számok összegeként nem kaphatunk 4-et.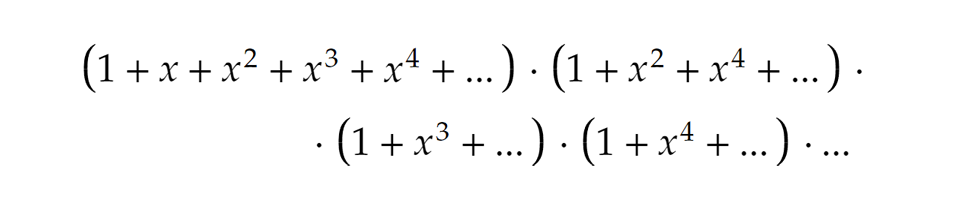Képzeljük el, hogy felbontjuk ezeket a zárójeleket, de koncentráljunk csak az x⁴ tagokra. Hogyan kaphatunk ilyet? Például, ha az első zárójelből az x⁴-t választjuk, az összes többiből az 1-eseket kell, hogy a szorzat negyedfokú lehessen: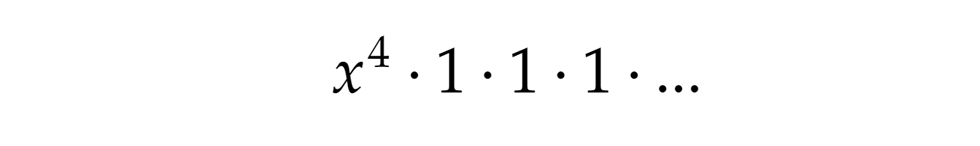A fentiek alapján ez felel meg az 1+1+1+1 („tiszta”) partíciónak, mivel az első zárójelből választottuk az x⁴-t, ahol csak 1-esekből építkezhetünk.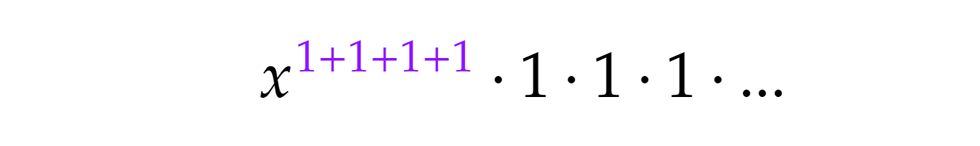Szintén x⁴-t kapunk, ha a második zárójelből választjuk az x⁴-t és az összes többiből az 1-est. Mivel a második zárójelből választottuk a negyedfokú tagot, ahol csak 2-eseket használunk, ez a 2+2 partíciónak felel meg.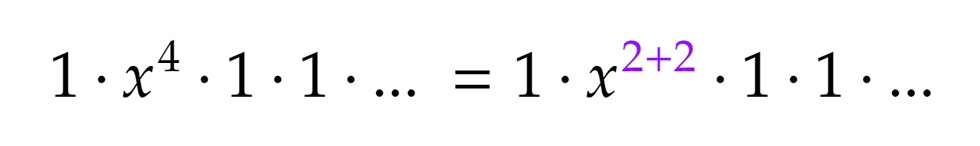Hasonlóan, ha a negyedik zárójelből választjuk az x⁴-t az összes többiből pedig 1-est, x⁴-t kapunk. Mivel a negyedik zárójelben vagyunk, az építőkockák 4-esek, tehát ez a verzió a triviális, azaz a 4 partíciót takarja.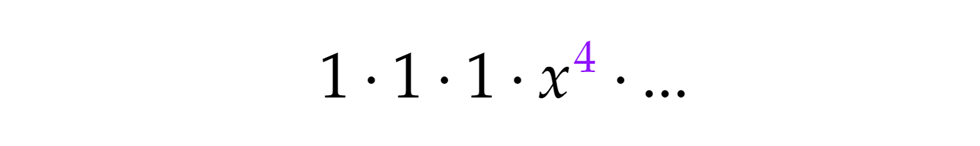Próbálkozzunk kisebb kitevőjű hatványokkal. Ha az x⁴-t egy harmadfokú és egy elsőfokú tag szorzatából szeretnénk előállítani, akkor az x³-t nem választhatjuk az első zárójelből, mert akkor kellene mellé egy elsőfokú x is valamelyik későbbiből, de ilyen már nem lesz. A másik lehetőség, hogy az x³-t a harmadik zárójelből választjuk, így az első zárójelből lesz mellé elsőfokú tag. Természetesen minden más zárójelből 1-est kell választani: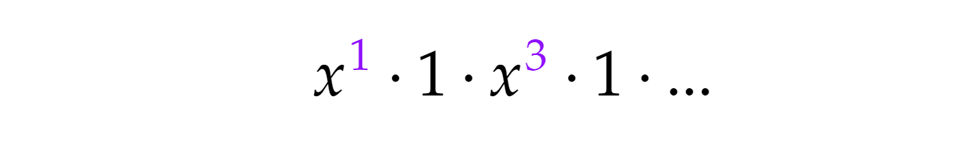Ez az eset az 1+3 partíciónak felel meg, mert az x az első zárójelből való, azaz az 1-et 1-esekből állítjuk elő (1=1), az x³ pedig a harmadikból, azaz a 3-at 3-asokból (3=3).

Folytassuk a sort, két x² szorzataként is kaphatunk x⁴-t. Ilyenek csak az első két zárójelben vannak, így értelemszerűen ezeket kell választanunk: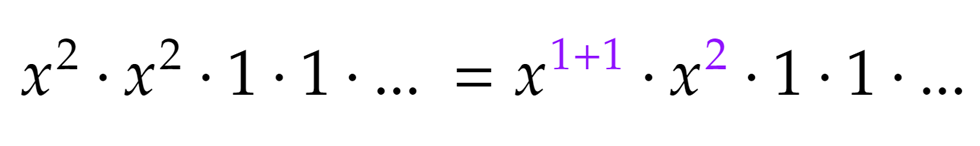Ez az 1+1+2 partíciót kódolja, ugyanis az első zárójelből választunk egy másodfokú tagot, azaz 1-esekből állítjuk elő a 2-t (1+1), illetve a másodikból a másik másodfokú tagot, ami a 2 csak 2-esekből történő előállítását takarja.

Ezzel a lehetőségek végére is értünk, az x⁴-es tagból összesen 5 darab lesz, és épp ennyi volt a 4 partícióinak száma is. Összefoglalva, a zárójel „sorszáma” azt jelzi, hogy milyen számokból építkezünk, a hatványkitevő pedig azt, hogy melyik számot bontjuk fel így épp, azaz esetünkben:

Az összetekert szárítókötél 

A fenti példában, ha ténylegesen elvégeztük volna a zárójelfelbontást, nem csak a negyedfokú tagokra figyeltünk volna, ugyanígy megkaptuk volna a többi természetes szám partícióinak számát is, ráadásul gyönyörűen felsorakozva egymás után. Egy adott n partícióinak száma a hozzá kapcsolható xⁿ együtthatója: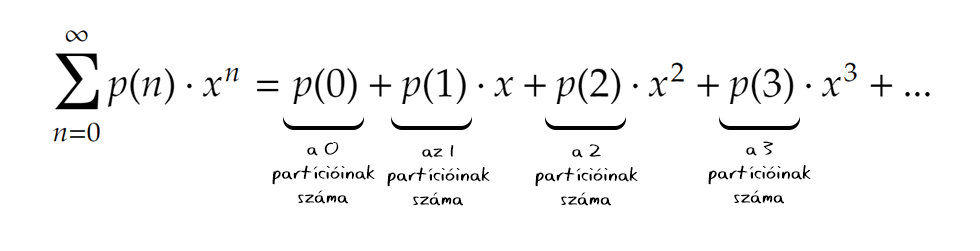
A hatványsorok konvergenciájának ismeretében a generátorfüggvény felírható tömörebb formában is. Mivel a szorzatban szereplő zárójelek végtelen geometriai sorok, ha |x|<1, akkor az összegük véges és kiszámítható a geometriai sor összegképlete alapján, azaz
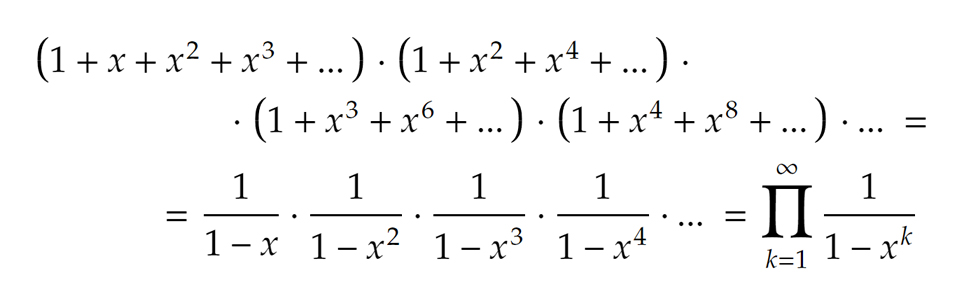Jegyezzük meg, hogy itt a konvergenciára is csak formálisan van szükségünk, az x értéke határozatlan és lényegtelen is.

Mindezen megpróbáltatások után, a generátorfüggvény birtokában térjünk vissza Euler másik, korábban említett felfedezésére.

Páratlan vs különböző összetevők

Emlékeztetőül, arról volt szó, hogy egy természetes számnak a csak páratlan számokat tartalmazó partícióinak száma megegyezik azon partícióinak számával, melyekben minden tag különböző.

A fentiek fényében, a csak páratlan számokból álló partíciókat megkaphatjuk úgy, ha a generátorfüggvényben csak minden második összeget (azaz a "páratlan sorszámú" zárójeleket) vesszük figyelembe, hiszen ezek esetén építkezünk páratlan számokból. Ismét csak a geometriai sor összegképletére hivatkozva ez nem más, mint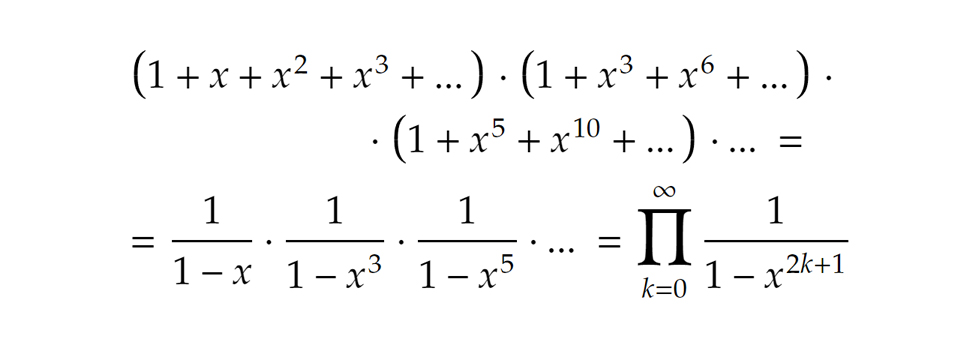A csak különböző tagokból álló partíciók számát kicsit nehezebb megfogni. Lényegében akkor beszélhetünk ilyenről, ha az egyes zárójelekből legfeljebb akkora kitevőjű tagot választunk, mint ami a zárójel „sorszáma”. Ha ugyanis nagyobbat választanánk, az azt jelentené, hogy az adott sorszámnak megfelelő szám előállítása tartalmazna legalább két egyforma tagot. Például a második összegből a negyedfokú tag választása két 2-est jelentene, a hatodfokúé hármat stb.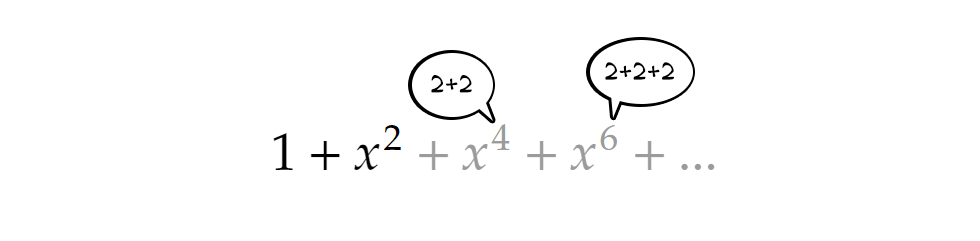Ez viszont akkor azt jelenti, hogy minden összegből csak az első két tag jöhet számításba, tehát a szorzatunk: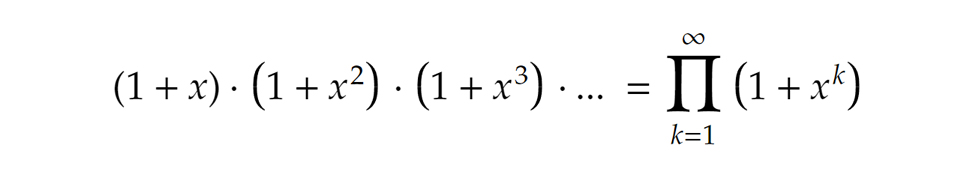Ebből egy kis algebrai trükkel élve (egész pontosan végtelenszer alkalmazva az a²-b² = (a+b)(a-b) azonosságot) az alábbit kapjuk: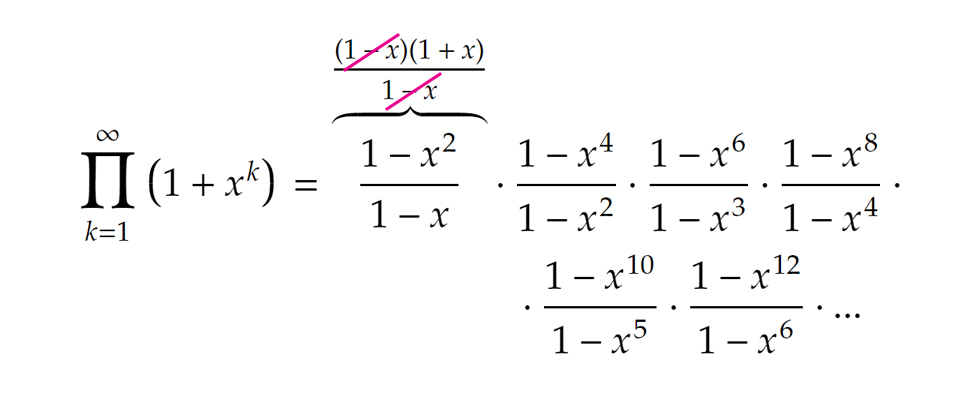Ha alaposabban szemügyre vesszük a jobb oldalt, láthatjuk, hogy a páros hatványokat tartalmazó kifejezések ki is esnek: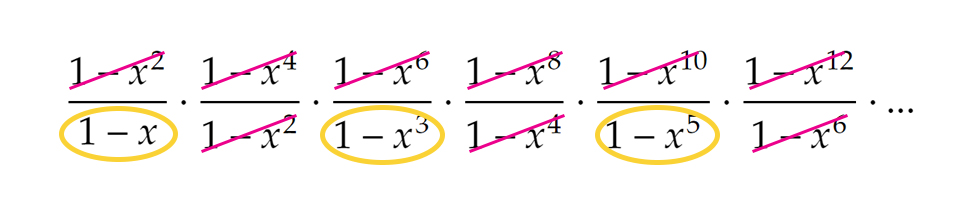ami marad, az pedig éppen a csak páratlan tagokra való bontásnál kapott képlet: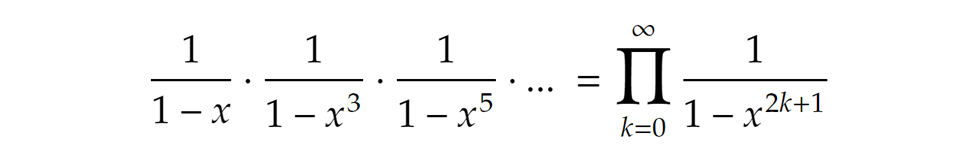Tehát a kétféle partíciók száma valóban ugyanannyi.

Az elődökre támaszkodva

Egy másik érdekesség, ami talán valamivel természetesebbnek is érződhet, hogy egy természetes szám partícióinak száma visszavezethető a nála kisebb számok partíciószámára, hiszen a kisebb számok előállítási lehetőségei kihatnak a következő számokéira is. Fontos lesz viszont közben figyelemmel kísérni a partíciók tagjainak számát.

Lássunk egy példát. A 11-nek a 2+2+3+4 négytagú partícióját tekintve, ha minden számból kivonunk 1-et, szintén egy négytagú összeget kapunk, ami épp a 11-nél 4-gyel kisebb szám, azaz a 7 egy partícióját adja: 1+1+2+3.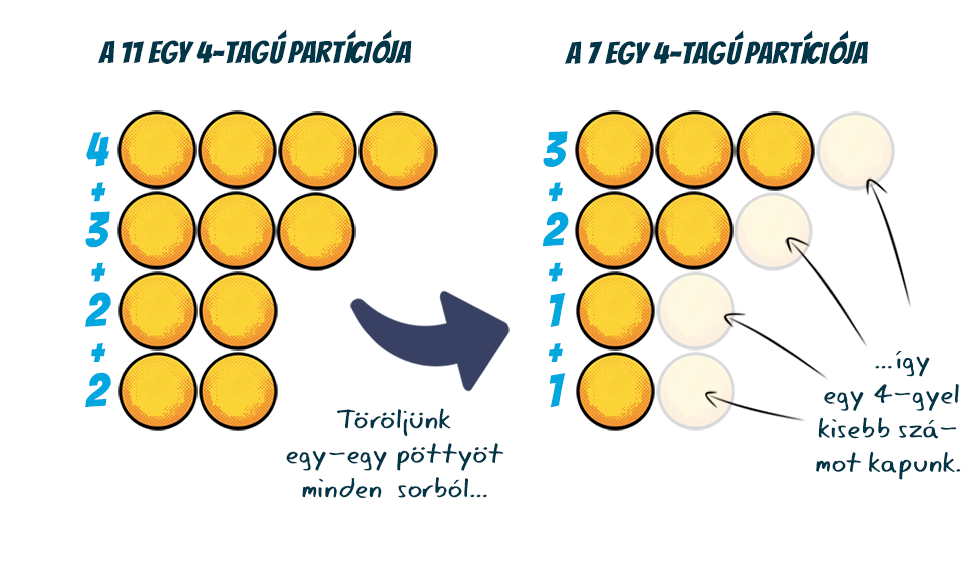Persze, ha az 1+1+4+5 partíciót néztük volna, ott a 3+4-et kapnánk, ami már egy kisebb elemszámú partíció, de továbbra is a 7-é.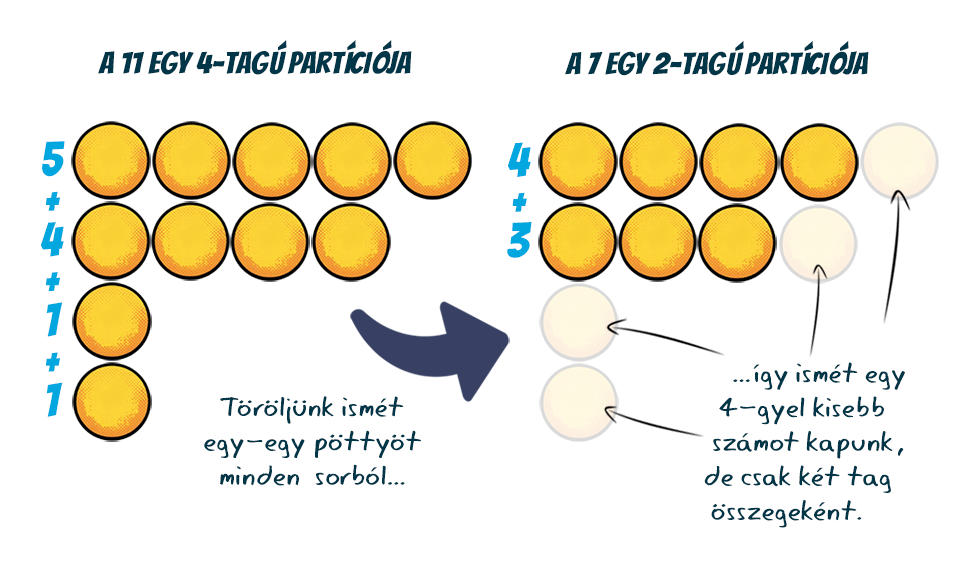Ami végeredményben levonható következtetésként, hogy egy szám adott k-tagú partícióinak száma ugyanannyi, mint a számnál épp k-val kisebb szám legfeljebb k-tagú partícióinak száma. (Az állítás bizonyítását mellőzzük, de az alapgondolat a fentinek megfelelő.)

Rekurzió

Pontosan hogyan is befolyásolják a kisebb számok partíciói a soron következő számét? Sokféleképpen közelíthetnénk, de mindenképpen csoportosítanunk kell a partíciókat a tagszámuk szerint. Ennek egy lehetséges módja, ha speciálisan csak az ugyanolyan és az eggyel kisebb tagszámú partíciókra koncentrálunk.

Visszatérve a 11 példájára, ha azokat a négytagú partícióit tekintjük, melyekben nincs 1-es, akkor minden tagból levonva 1-et a tagszám nem változik, csak az összeg, azaz pontosan a 7 négytagú partícióit kapjuk, ahogyan az imént már láttuk. Más szóval, a 11-nek az 1-eseket nem tartalmazó négytagú és a 7 (bármilyen) négytagú partíciói kölcsönösen egyértelműen párosíthatók.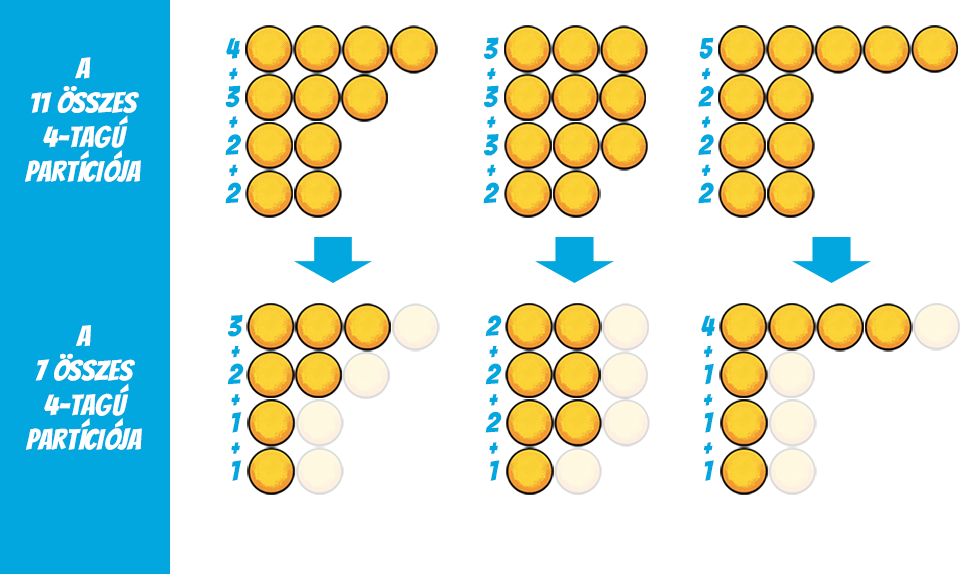

A 11 azon partícióinál pedig, melyek tartalmaznak 1-est, hagyjuk el az egyiket, így mindig a 10 egy eggyel kisebb tagszámú partícióját kapjuk. Ezek szintén kölcsönösen egyértelműen megfeleltethetőek egymásnak.

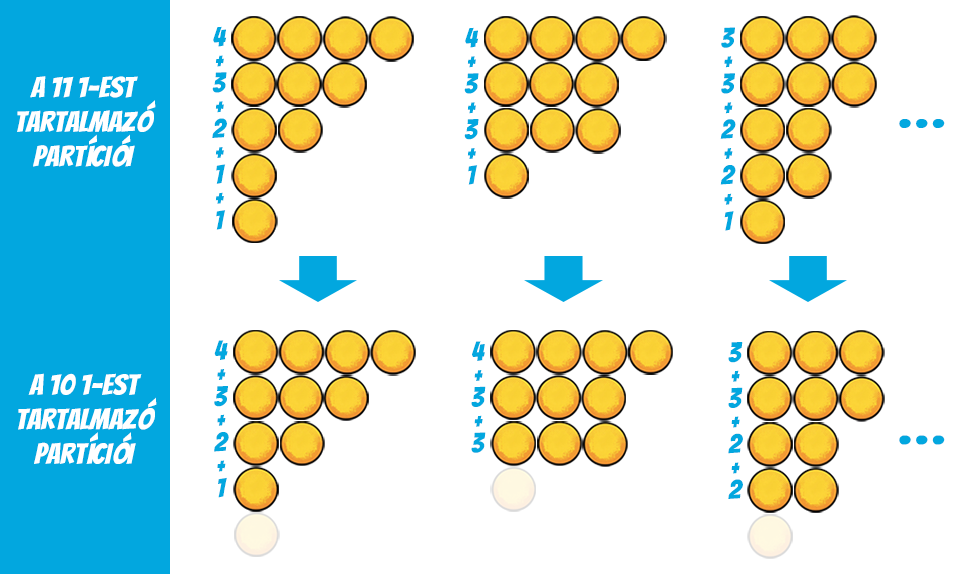
Mivel egy partíció vagy tartalmaz 1-est vagy nem, ezzel minden lehetőséget le is fedtünk. Ráadásul a két kategória között nincs átfedés, így attól sem kell tartanunk, hogy valamit többször vettünk számításba. Általánosságban tehát, ha egy n természetes szám k-tagú partícióinak száma p_k(n), akkor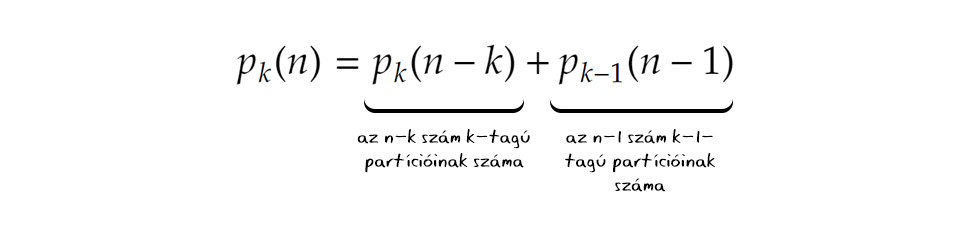

Irány a végtelen

A generátorfüggvény segítségével ugyan bármely természetes szám partíciószáma meghatározható, de egyáltalán nem nevezhetjük hatékonynak a módszert. Például a 100 esetén a 100. kitevős hatványok összegyűjtése nem egy kellemes feladat. Ha gyorsaságot akarunk, annak ára van, mégpedig – ahogy az lenni szokott – a pontosság.

A partíciók számának becslése kérdésében a 20. század elején áttörés történt. Ez az áttörés India egyik legnagyobb tehetségének, Srínivásza Rámánudzsannak és professzorának, Godfrey Harold Hardy-nak volt köszönhető. 1918-ban publikálták azt a cikküket, melyben aszimptotikus közelítést adtak a partíciók számára vonatkozóan. (Az esetről egyébként remek film is készült Az ember, aki ismerte a végtelent címmel.) A képlet maga mellesleg a következő: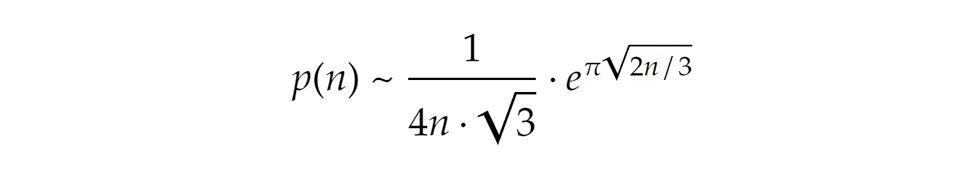ahol n jelöli azt a számot, aminek a partícióiról szó van, p(n) pedig a partíciók számát.

A formula kis számokra persze nem túl pontos. Például a 4-re tudjuk, hogy a partícióinak száma 5, a fenti képlet szerint viszont 6,1. A 100 esetében azonban, melynek összesen 190 569 292 partíciója van, a fenti közelítés kb. 199 280 893-at eredményez, ami látszólag szintén hatalmas eltérés, de ha arányaiban nézzük, kevesebb mint 4,6%, míg a 4-nél ugyanez az érték 22% volt.

A képlet kapcsán egyébként nem mehetünk el szó nélkül Percy Alexander MacMahon neve mellett sem, aki fáradságos munkával meghatározta a természetes számok partícióinak számát egészen 200-ig, remek ellenőrzési pontot nyújtva ezzel Rámánudzsanék számára.

A fenti képletet Hardy és Rámánudzsan később tovább finomította. A bizonyítások sajnos mindkét esetben komoly komplex analízisbeli eszközöket használnak, és jócskán bonyolultabbak annál, minthogy itt kifejthessük őket.

Oszthatóság

Rámánudzsan érdeme nem merül ki a fentiekben, nem mintha az önmagában nem lenne hatalmas eredmény. Levezetett néhány olyan összefüggést is, ami bizonyos számok partíciószámának oszthatóságával kapcsolatosak.

Ilyen például, hogy az 5n+4 alakú számok partícióinak száma mindenképpen 5-tel osztható szám (lásd például a 4 esetét). Hasonlóan, a 7n+5 alakúaké 7-tel, a 11n+6 alakúaké pedig 11-gyel osztható. Mindezek kongruenciákként felírva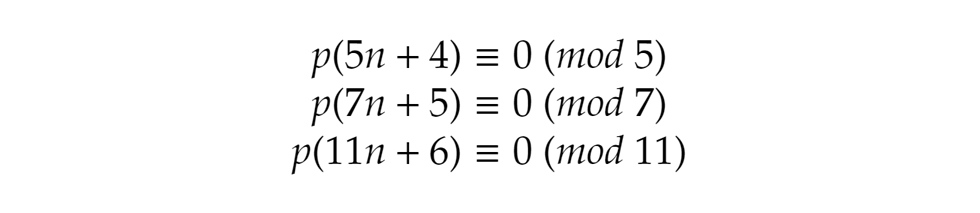Ezek bizonyítása szintén meghaladja e bejegyzés kereteit, de akit bővebben érdekel, megtalálja például itt vagy itt.

Erdős

Zárásként, de messze nem utolsósorban említsük meg, hogy a zseniális és sokoldalú 20. századi magyar matematikus, Erdős Pál is letette névjegyét a partíciók területén. Erdős Rámánudzsan és Hardy formulájához hasonlót vezetett le 1942-es cikkében. Bizonyításának fő erénye, hogy mellőzi a komplex függvénytani ismeretek használatát. Igaz, a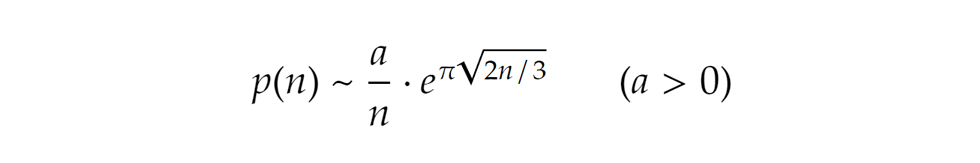képlet csak annyit mond, hogy valamely pozitív a-ra teljesül az aszimptotikus egyenlőség, magát az a-t nem határozza meg. (Rámánudzsanék esetén ugye a=1/(4√3).) A bizonyítás ez esetben sem épp egyszerű vagy rövid, akit érdekel, részleteiben például itt megtalálhatja.

Variációk egy témára

Messzire kalandoztunk a számok építését megcélzó alapgondolatunkkal, noha a kiindulópontunk egyszerű volt, pusztán az 1-es szám és az összeadás művelete kellett hozzá. Számokat alkotni persze sok más módon is lehet. Hamarosan bemutatunk egy másik lehetőséget is, ami annyiban különbözik majd, hogy az összeadást szorzásra cseréljük, az 1-est pedig más számokra, de a bejárt út hasonlóan érdekes lesz. Ez viszont már egy másik történet.

 Források:

 https://mathworld.wolfram.com/FerrersDiagram.html

https://uli.rocks/p/generating-functions/

https://en.wikipedia.org/wiki/Generating_function

https://artofproblemsolving.com/wiki/index.php/Partition_(combinatorics)

https://zenodo.org/records/1447425

https://en.wikipedia.org/wiki/Generating_function#Congruences_for_the_partition_function

https://users.renyi.hu/~p_erdos/1942-02.pdf